다음 포스팅은 https://youtu.be/GPiaq1zxXlg 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
지난시간
정의 (선형연산) 집합 A위에 다음의 두가지 연산이 주어질때 이 연산들을 선형연산이라 부른다.
1) 덧셈: 집합 A의 임의의 두 원소 $x,y$에 대해서 $x+y∈A$ 우리는 집합 A를 덧셈에 대한 군 (group)이라고 가정한다.
2) 스칼라곱: 집합 A의 임의의 원소 $x$와 임의의 실수 $r$에 대해 $r·x∈A$ 이때 0,$x$=0으로, 1·$x$=$x$로 정의한다.
선형연산이 주어진 집합 A를 벡터공간 (Vector Space)라 부르며, 벡터공간의 원소를 벡터 (Vector)라고 부른다.
두 벡터 공간 A,B에 대하여 함수 $f:A\Longrightarrow$B가 다음의 조건을 만족하면 선형함수라고 부른다:
A의 임의의 두 벡터 $x,y$와 임의의 두 실수 $a,b$에 대하여
$f(a \cdot x+b \cdot y)=a \cdot f(x)+b \cdot f(y)$를 만족한다.
예시 실수집합 $\mathbb(R)$의 임의의 원소 $x,y$에 대해 순서쌍 $(x,y)$의 모임 ${(x,y):x\in\mathbb{R},y\in\mathbb{R}}$ 을 $\mathbb{R^2}$로 명시하자
$\mathbb{R^2}$는 아래와 같이 덧셈과 스칼라곱이 잘 정의되므로 벡터공간이다:
덧셈) $)\left(x_{1}, y_{1}\right)+\left(x_{2}, y_{2}\right)=\left(x_{1}+x_{2}, y_{1}+y_{2}\right)$
스칼라곱} $r \cdot(x, y)=\left(r x_{1} r y\right)$
선형함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$,
$\begin{aligned}& f((x, y))=(ax+by,cx+by)\end{aligned}$는
$f\left(\left(\begin{array}{l}x \\y\end{array}\right)\right)=\left(\begin{array}{ll}a & b \\c & d &\end{array}\right)\left(\begin{array}{l}x \\y\end{array}\right)$, 즉 2×2 행렬 $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$과의 행렬곱으로 표현된다.
일반적인 함수들의 경우 (군의 관점)
결합법칙 세 함수 $f:A\Longrightarrow$B, $g:B\Longrightarrow$C, $h:C\Longrightarrow$D에 대해서 $(h\circ{g})\circ{f}=h\circ(g\circ{f})$:$A\longrightarrow$D 를 만족한다.
항등원 임의의 함수 $f:A\longrightarrow$A에 대해서 항등함수 $I_A:A\longrightarrow$B
$x|\longrightarrow$x
는 $f \circ 1_{A}=1_{A} \circ f=f$를 만족한다.
역원 만약에 함수 $f:A\longrightarrow$A가 전단사 함수이면, 역함수 $f^{-1}:A\longrightarrow$A가 존재하여, 역함수 $f \circ f^{-1}=f^{-1} \circ f=I_{A}$를 만족한다.
마법 선형함수들 간의 합성은 선형함수들이 만들어내는 행렬들의 곱셈과 같았다. 즉 두 선형함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$,$g: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$를
$
f\left(\left(\begin{array}{l}
x \\
y
\end{array}\right)\right)=\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)
$= $\left(\begin{array}{ll}p & q \\r & s\end{array}\right) \stackrel{}{=}\left(\begin{array}{ll}x \\y \end{array}\right)$로 두면
$
\begin{aligned}
& g \circ f\left(\left(\begin{array}{l}
x \\
y
\end{array}\right)\right)=\left(\begin{array}{ll}
* & * \\
* & *
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right) \text { 에서 }\left(\begin{array}{ll}
* & * \\
* & *
\end{array}\right) \text { 는 }
\end{aligned}
$
정확히 $B$와 $A$의 행렬곱 $B×A=BA$가 된다 (지난 시간에 예시를 통해 확인). 그러므로 군의 관점에서 다름을 생각해보는게 자연스럽다.
2×2 행렬들의 경우 (군의 관점)
결합법칙 2×2행렬 $A,B,C$에 대하여 (각 행렬은 선형함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$로 볼 수 있음을 전제하고 있습니다)
$(A×B)×C=A×(B×C)$이다. 곱셈의 순서가 차이를 만들지 않음으로 괄호를 생략하고 $A×B×C$ 혹은 $ABC$로 표현해도 된다.
항등행렬 행렬 $\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$은 임의의 2×2행렬 $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$에 대하여
$\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)=\left(\begin{array}{ll}a & d \\ c & d\end{array}\right)$ 이다.
행렬 $\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$을 항등행렬 (identity matrix)라고 부른다.
역행렬 (이 렉쳐의 메인 스토리)
행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$에 대해 만약에 어떤 행렬 X$$가 존재하여
$A X=X A=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$이 성립한다면 $X$를 $A$의 역행렬 이라 부르고 $X=A^{-1}$로 표기한다.
질문 함수들의 모임에서 각 함수의 역함수가 존재하지 않을 수 있었듯이, 행렬들의 모임에서 역행렬 또한 일반적으로 존재하지 않습니다. 역함수가 존재하는 함수는 반드시 전단사함수인 것처럼, 역행렬이 존재하는 행렬은 매우 특별한 행렬일 것입니다. 이러한 행렬들은 어떠한 행렬들일까요?
아직 별 단서가 없으니 먼저 직접 역행렬을 찾으려고 시도해봅시다:
$
\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{ll}
(1) & (2) \\
(3) & (4)
\end{array}\right) \stackrel{?}{=}\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right) \text { 이 되어야함 }
$
우리는 위 식을 만족하는 (1),(2),(3),(4),가 무엇인지 알고 싶다.
$
\left(\begin{array}{ll}
a(1)+b(3) & a(2)+b(4) \\
c(1)+d(3) & c(2)+d(4)
\end{array}\right) \stackrel{?}{=}\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right) \text { 이 되어야함 }
$
$
\begin{aligned}
& \Leftrightarrow a(1)+b(3)=1 \\
& a(2)+b(4)=0, \Leftrightarrow a(2)=-b(4),(2)=-\frac{b}{a}(4) \\
& C(1)+d(3)=0, \Leftrightarrow C(1)=-d(3),(1)=-\frac{d}{c}(3) . \\
& c(2)+d(4)=1\\
& \Rightarrow\left\{\begin{array}{l}
a\left(-\frac{d}{c}(3)\right)+b \text { (3) }=1 \\
c\left(-\frac{b}{a}(4)\right)+d(4)=1
\end{array}\right.
\end{aligned}
$
(3),(4)로 각각 묶어서 정리하면
(3) $\left(\frac{-a d}{c}+b\right)=1, \frac{-a d+b c}{c}$ (3) $=1$, (3) $=\frac{C}{-a d+b c}$=$\frac{-C}{ad-bc}$
(4) $\left(\frac{-b c}{a}+d\right)=1, \frac{-b c+a d}{a}(4)=1$, (4) $=\frac{a}{a d-b c}$
(3),(4)를 알아냈으므로 이제 위의 빨강색, 보라색 관계식에 의해
(1) $=-\frac{d}{c}(3)=\frac{d}{a d-b c}$
(2) $=-\frac{b}{a}(4)=\frac{-b}{a d-b c} 이다$
그러므로 (1), (2), (3), (4) 를 다 알았다. 즉,
$\left(\begin{array}{ll}(1) & \text { (2) } \\ \text { (3) } & \text { (4) }\end{array}\right)=\left(\begin{array}{cc}\frac{d}{a d-b c} & \frac{-b}{a d-b c} \\ \frac{-c}{a d-b c} & \frac{a}{a d-b c}\end{array}\right)=\frac{1}{a d-b c}\left(\begin{array}{cc}d & -b \\ c- & a\end{array}\right)$ 이다.
찾은
$\left(\begin{array}{ll}(1) & \text { (2) } \\ \text { (3) } & \text { (4) }\end{array}\right)$가
$\left(\begin{array}{ll}a& \text {b} \\ \text {c } & \text {d}\end{array}\right)\left(\begin{array}{cc}1 & 2 \\ 3 & 4\end{array}\right)=\left(\begin{array}{cc}1 & 0 \\0 & 1\end{array}\right)$ 임은 위의 계산으로부터 알았고,
$\left(\begin{array}{ll}1 & \text {2} \\ \text { 3 } & \text { 4 }\end{array}\right)\left(\begin{array}{cc}a & b \\ c & d\end{array}\right)=\left(\begin{array}{cc}1 & 0 \\0 & 1\end{array}\right)$ 도 성립하는지 확인해보자:
$
\begin{aligned}
& \frac{1}{a d-b c}\left(\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right)\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right) \stackrel{행렬곱}{=} \frac{1}{a d-b c}\left(\begin{array}{cc}
a d-b c & 0 \\
0 & a d-b c
\end{array}\right) \\
& \text { || 행렬의 스칼라곱 } \\
& \frac{1}{\operatorname{ad}-bc} \cdot(\operatorname{ad}-bc)\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right) \\
&\text { || ad-bc 약분 } \\
& \left(\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right) \text { 이다 }
\end{aligned}
$
그러므로 $\frac{1}{a d-b C}\left(\begin{array}{cc}d & -b \\ -c & a\end{array}\right)$ 는 $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$의 역행렬이다.
관찰들 (1) 2×2행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$에 대하여 $A$의 역행렬 $A^-1$는 $\frac{1}{a d-b C}\left(\begin{array}{cc}d & -b \\ -c & a\end{array}\right)$ 여야만 한다. 그런데 역행렬 앞에 $ad-bc$가 분모로서 붙어있음에 주목하자.
2번째 주의 렉쳐의 계산문제들 중에 분수에서 분모가 0일 수 없음에 대해 살펴보았다. (가령 $\frac1{0}$이 정의되려면 $1=\frac1{0}\times0=0$이다)
그런데 $a,b,c,d$중에서 얼마든지 $ad-bc=0$인 숫자들이 존재한다. 이 경우에는 역행렬이 정의될 수 없을 것이다.
우리는 다음의 사실을 알아낸 것이다:
행렬 $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$의 역행렬이 존재하는 "필요중분조건"은
$ad-bc$가 /$0$이 아닌 것이다.
우리는 이 특별한 숫자 $ad-bc$를 행렬식 (determinant)라고 부르며, det$A$로도 많이 적는다.
(2) 그림으로서의 관찰
행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$는 함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$,
$
\begin{aligned}
& f\left(\left(\begin{array}{l}
x \\
y
\end{array}\right)\right)=\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)=(a x+b y, c x+d y)
\end{aligned}
$
에서 왔던 것임을 상기해보자: 여기서 $ax+by,cx+dy$는 벡터공간 $\mathbb{R}^{2}$의 선형연산 (덧셈, 스칼라곱)으로 만들어진 것이다.
$\mathbb{R}^{2}={(x,y)|x,y\in\mathbb{R}}$은 2차원 평면으로서 다음과 같이 그릴 수 있다:
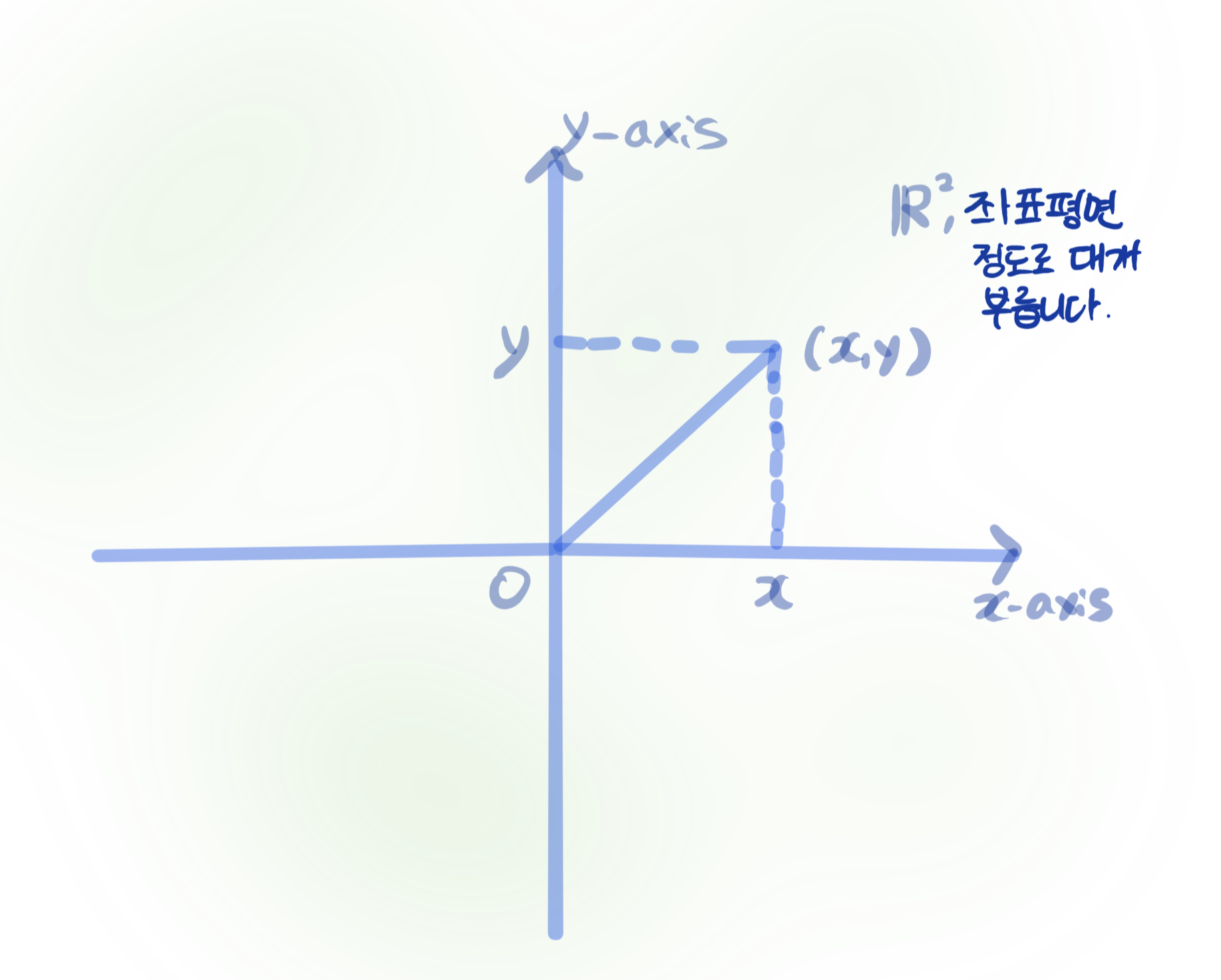
그림상에서, $f\left(\left(\begin{array}{l}x \\ y\end{array}\right)\right)=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)\left(\begin{array}{l}x \\ y\end{array}\right)$가 하고 있는 일:
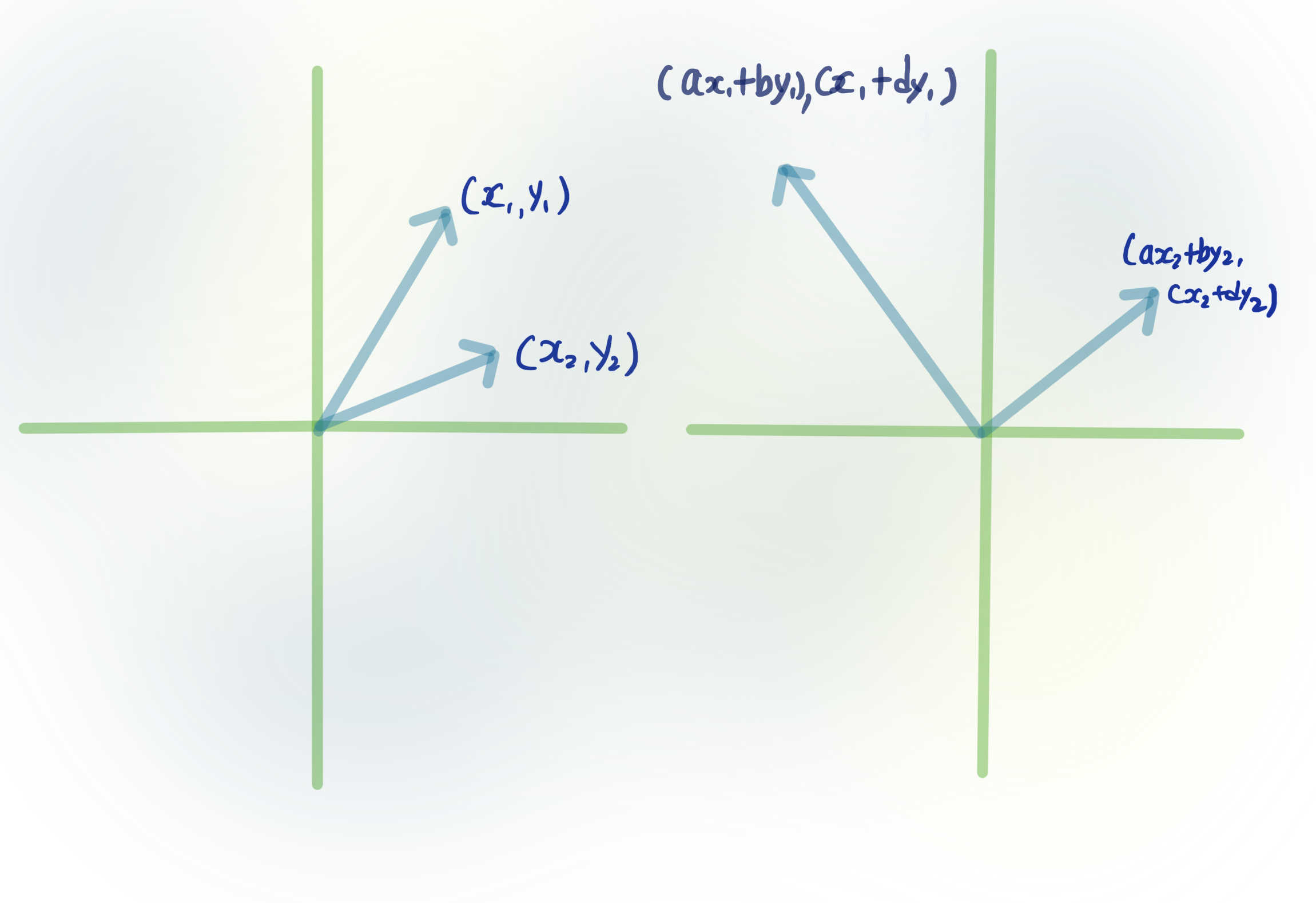
해석 정의역 $\mathbb{R}^{2}$의 벡터들, 가령 $(x_1,y_1)$, $(x_2,y_2)$를 이미 정해진 $a,b,c,d$값을 따라서
$(ax_1+by_1, cx_1+dy_1). (ax_2+by_2, cx_2+dy_2)$로 (선형적으로) 옮겨주고 있다.
여기서, $a,b,c,d$ 값이 각 $x$성분과 $y$성분을 선형적으로 얼마나 키워주거나 줄일지, 방향을 바꿀지를 결정해준다.
(3) (행렬식 $ad-bc$의 기하학적 의미)
행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$가 주어져 있다고 가정하자.
그런데 $\left(\begin{array}{ll}a& \text {b} \\ \text {c } & \text {d}\end{array}\right)\left(\begin{array}{cc}x \\ y \end{array}\right)=\left(\begin{array}{cc}ax+by\\ cx+dy\end{array}\right)$에서 $a,b$와 $c,d$가 계산에 사용되는 위치가 다름을 알수있다. 그러므로 따로 두 순서쌍 $(a,b)$와 $(c,d)$를 고려하자. 이들은 $\mathbb{R}^{2}$의 원소이므로 다음과 같이 좌표평면 위에 그릴 수 있다:
주장 행렬식 $ad-bc$는 두 벡터 $(a,b)$와 $(c,d)$가 만들어내는 평행사변형의 면적에 해당한다. 즉,
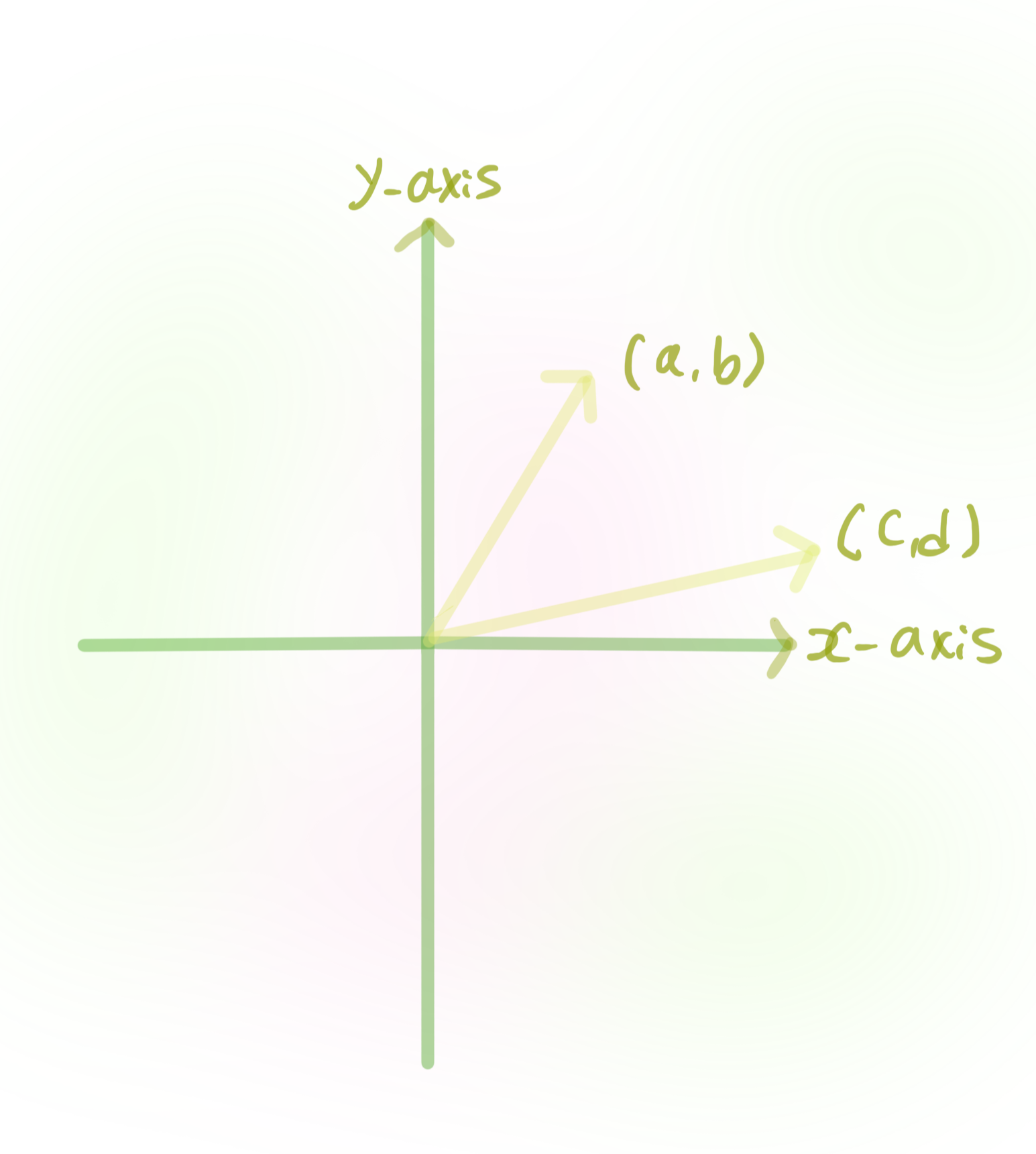
(이 주장의 증명은 삼각함수와 회전행렬을 사용합니다. 다음 렉쳐에서 상세히 다루겠습니다.)
(4) 이제 관찰 (1),(2),(3)을 종합하여 보자.
2×2 행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$가 주어져 있다고 가정하자.
이 행렬이 주어졌다는 것은 선형함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$
$f\left(\left(\begin{array}{l}x \\ y\end{array}\right)\right)=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)\left(\begin{array}{l}x \\ y\end{array}\right)$=$\left(\begin{array}{l}a x+b y \\ c x+d y\end{array}\right)$
가 주어졌다는 말과 같은 것이다. 그런데 네 번째 렉쳐로부터, 우리는 $f$의 역함수 $f^-1$가 주어질 필요 충분조건은
$f$가 전단사 함수라는 것을 알았다.
그런데 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$가 선형함수이고 전단사 함수이면
$f^-1: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$도 반드시 선형함수여야 한다. (연습문제)
$f\circ{f}^-{1}=f^-1\circ{f}=id_\mathbb{R}^{2}$의 관계를 $f,f^-1$에 대응하는 행렬들 $A,B$및 이들의 행렬과
$AB$=$BA$=$\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$
이 되어야 함을 다섯번째 렉쳐에서 보았다.
즉 $f^-1$에 대응하는 행렬 $B$는 반드시 $A$의 역행렬 이어야 한다.
그런데 우리는 관찰 (1)로 부터 행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$의 역행렬이 존재하는 필요충분조건은 det$A=ad-bc≠0$임을 알았다.
즉, 우리는 함수
$
f\left(\left(\begin{array}{l}
x \\
y
\end{array}\right)\right)=\left(\begin{array}{ll}
ax+by \\
cx+dy
\end{array}\right)
$
가 전단사 함수일 필요충분 조건이 $ad-bc≠0$을 안다는 뜻이다.
이는 어떤 함의를 갖는가? 관찰 (3)으로부터 $ad-bc$는 두 벡터 $(a,b)$와 $(c,d)$가 만들어내는 평행사변형의 면적임을 알았다. 즉 함수 $f$가 전단사함수 라는 것은 두 벡터 $(a,b)$,$(c,d)$가 만드는 평행사변형의 면적이 0 이 아님과 같다는 것이다.
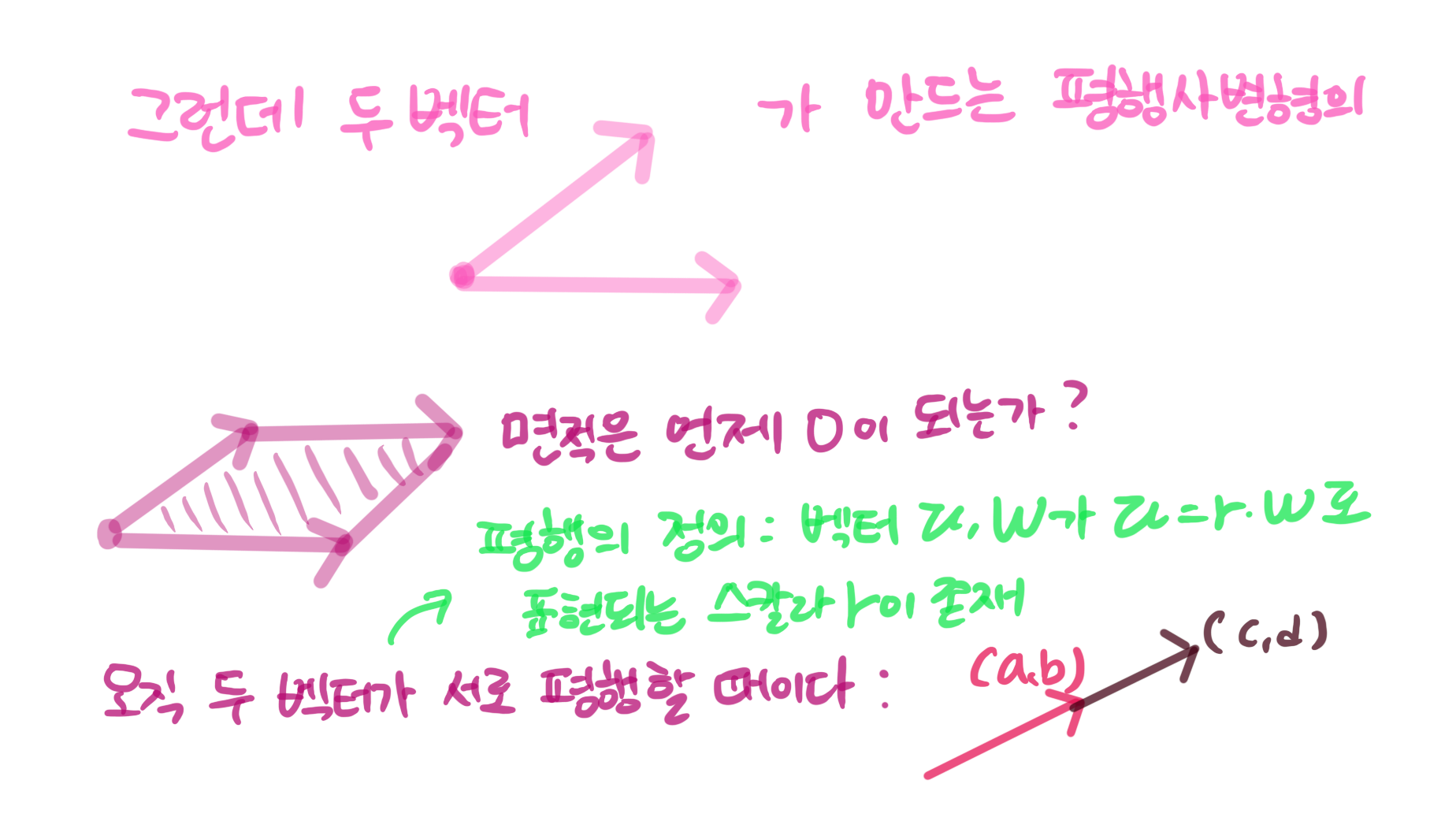
(5) 지금까지의 한 말을 간결히 정리하면 아래와 같다:
선형함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$,
$
f\left(\left(\begin{array}{l}
x \\
y
\end{array}\right)\right)=\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)
$
가 역함수 $f^-1$가 존재할 필요충분조건은 두 벡터 $(a,b)$와 $(c,d)$가 서로 평행하지 않을 때 이다.
이 경우 역함수 $f^-1: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$에 대응되는
역행렬 $A^-1$은
$
\begin{aligned}
& \frac{1}{\operatorname{ad}-bc}\left(\begin{array}{ll}
d & -b \\
-b & a
\end{array}\right) \\
\end{aligned}
$로 주어진다.
코멘트 행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$를 이해하려고 애쓰시는 과정에서 어는 순간부터 지식과 논리만이 아니라 그림과 직관도 함께 머리속을 채우고 계시지 않나요? 만약에 그러하시다면, 실로 환영합니다. 여러모로 상상하시며 누리고 즐기시길 빕니다. 지금까지의 관찰을 군의 관점에서도 살펴봅시다.
군으로서의 행렬의 모임
다음의 집합 $S$를 정의하자
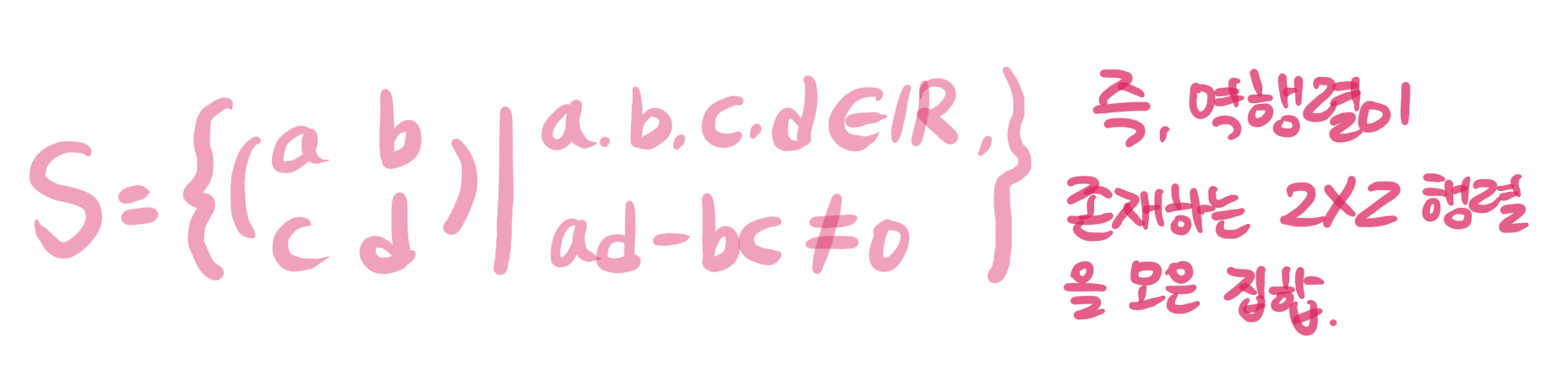
$S$는 행렬간의 곱셈을 연산으로 갖는 군이 된다.
결합법칙: 임의의 2×2 행렬 $A,B,C$에 대하여
$(AB)C=A(BC)$가 성립한다.
항등원: $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)=\left(\begin{array}{ll}1 & 0 \\ 0 &
1\end{array}\right)\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)=\left(\begin{array}{ll}a & d \\ c & d\end{array}\right)$
역원: $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$∈$S$의 역원은
$A^-1$=$
\begin{aligned}
& \frac{1}{\operatorname{ad}-bc}\left(\begin{array}{ll}
d & -b \\
-b & a
\end{array}\right) \\
\end{aligned}
$
$S$의 각 원소 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$마다 0이 아닌 $(ad-bc)$ 값을 갖는다. 즉, 우리는 다음과 같은 함수를 정의할수 있다:
det: $S\longrightarrow\mathbb{R}-\{0\} ({0}= 0이 아닌 실수의 모임)
$A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ det$A$=$ad-bc$
연습문제 (행렬곱과 행렬식의 정의만 가지고 직접 계산해 보세요)
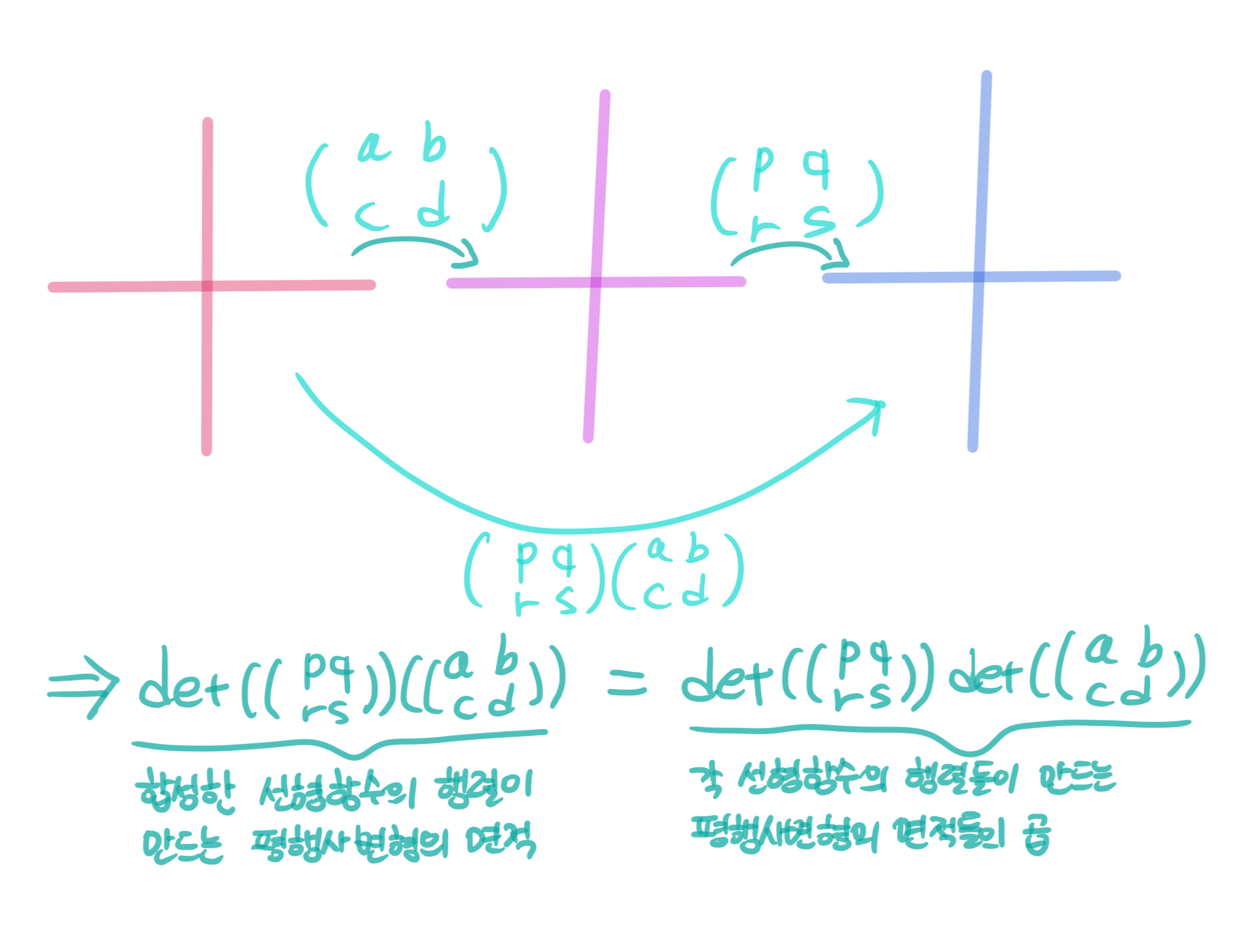
(1)det $\left(\begin{array}{ll}1 & 2 \\3 & 4\end{array}\right) \stackrel{}{}\left(\begin{array}{ll}5 & 6 \\7 & 8\end{array}\right) \text {}$=det $\left(\begin{array}{ll}1 & 2 \\ 3 & 4\end{array}\right)$ det $\left(\begin{array}{ll}p & q \\ r & s\end{array}\right)$
(2) det $
\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right) \stackrel{}{}\left(\begin{array}{ll}
p & q \\
r & s
\end{array}\right) \text {}
$=det $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ det $\left(\begin{array}{ll}p & q \\ r & s\end{array}\right)$
(3) det $\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$=1
(4) det$
\begin{aligned}
& \frac{1}{\operatorname{ad}-bc}\left(\begin{array}{ll}
d &-b \\
-b & a
\end{array}\right) \\
\end{aligned}
$= $
\begin{aligned}
& \frac{1}{\operatorname{ad}-bc}
\end{aligned}
$
중요한 질문 위의 연습문제들이 무슨 뜻을 갖는지 혹시 눈치 채셨나요?
이미 똑같은 관찰을 3,4,5주 렉쳐 속에서 매우 중요하게 다루었습니다.
답 행렬식 det $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$=$ad-bc$는 XXX를 보존하는 함수이다.
심화 가령 3×3 행렬처럼, 2×2 행렬보다 크기가 큰 경우에는 지금까지 한 이야기를 똑같이 반복할수 있을까요?
예 맞습니다.
단 2×2 행렬과 3×3 행렬보다 크기가 더 커진 행렬들을 다루는 경우에는 3차원 이상을 시각적으로 인지할 수 없는 인간의 인지 한계상 이 영역들은 오직 연산(대수)의 타당성을 힘입는게 인간이 할 수 있는 최선일 것입니다.
그렇다면 가령 3×3 $\left(\begin{array}{ll}a & b &c \\ d & e &f \\ g& h &i \\\end{array}\right)$ 행렬 의 행렬식은 어떻게 이해해야 우리가 본 2×2 행렬에서의 관촬과 consistent할까요?
2×2행렬 $A=\left(\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right)$ 의 행렬식 $+a_{11}a_{22}-a_{12}a_{21}$
부터 다시 살펴봅시다. $+a_{11}a_{22}-a_{12}a_{21}$ 는,
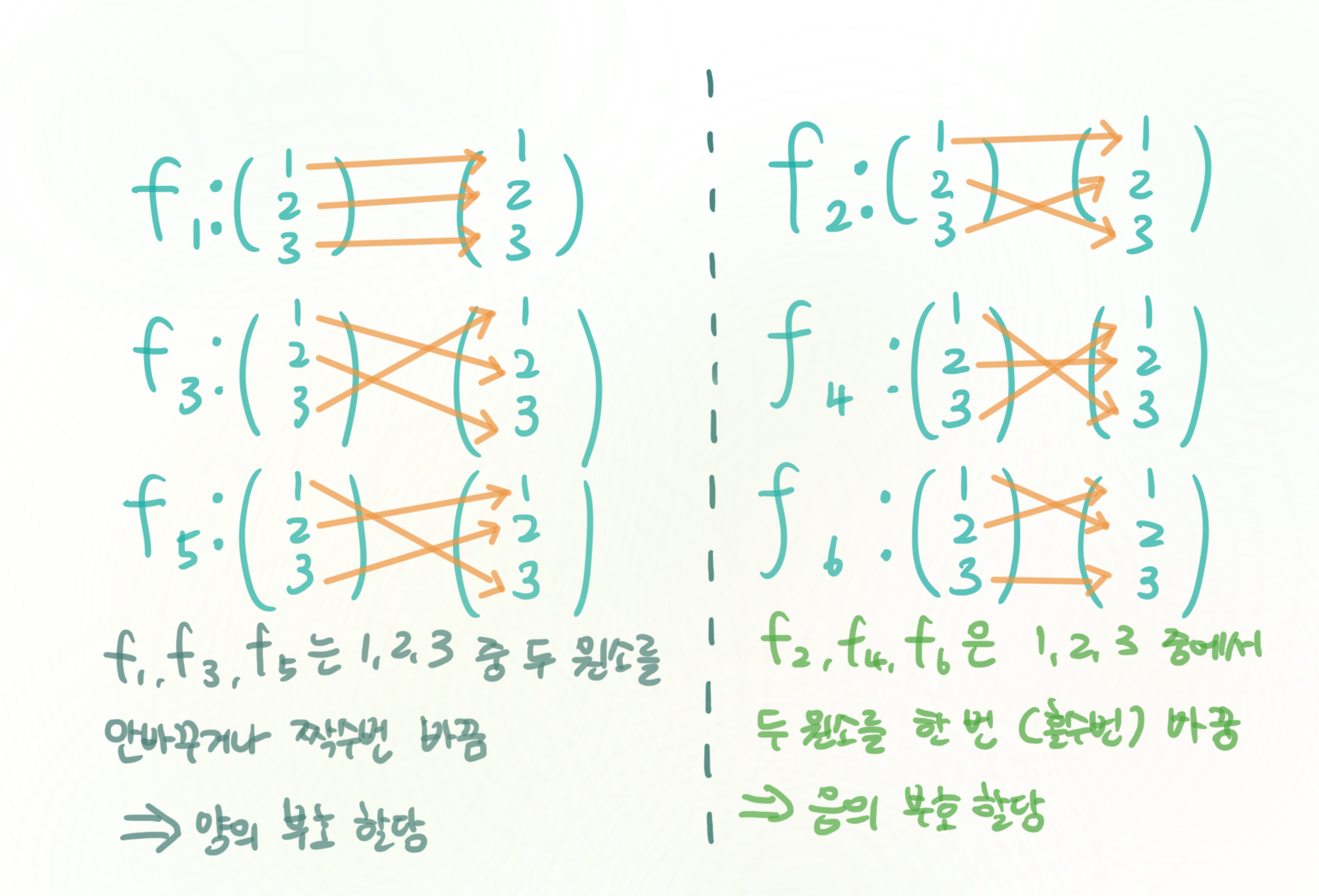
2차 대칭군 $S_2=\{f:\{1,2\}\longrightarrow\{1,2\}$ |$f 는 전단사 함수\}$
의 두 원소 $f_1:\{1,2\}\longrightarrow\{1,2\}$ ,1|$\longrightarrow1$
$2|\longrightarrow2$
$f_2:\{1,2\}\longrightarrow\{1,2\}$ ,1|$\longrightarrow2$
$2|\longrightarrow1$
에서 $f_1$은 1,2의 순서를 바꾸지 않아서 양의 부호를, $f_2$는 1과 2를 한번만 바꾸어서 음의 부호를 할당한 것으로 간주할 수 있습니다.
이 관찰을 3×3행렬에 적용하면,
3차 대칭군 $S_3=\{f:\left(\begin{array}{ll}1 \\2 \\3\end{array}\right) \longrightarrow\left(\begin{array}{ll}x \\y \end{array}\right)$
는 총 6개의 함수로 이루어져 있다:
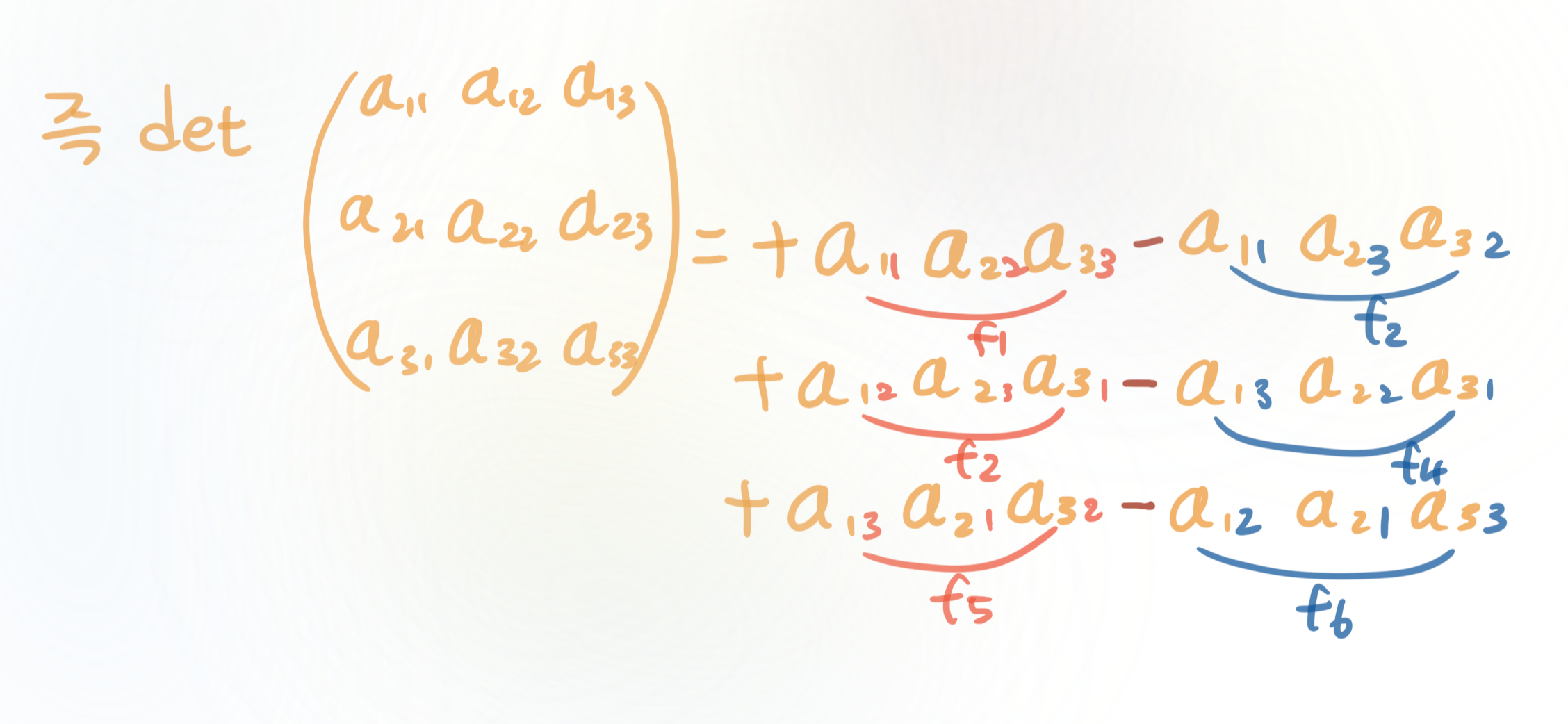
다음시간 삼각함수, 회전행렬, 고유치, 고유값
'직장인과 문과생을 위한 수학교실 (직문수)' 카테고리의 다른 글
| 8강. 선형대수학의 꽃, 무지개 정리 (0) | 2023.08.04 |
|---|---|
| 7강. 선형대수학과 기하학 (0) | 2023.08.03 |
| 5강. 벡터공간과 행렬, 선형대수학 Part 1 (0) | 2023.08.02 |
| 4강. 군의 관점에서 살펴보는 지수법칙과 역함수 (0) | 2023.08.02 |
| 3강. 함수의 정의와 군 (0) | 2023.08.01 |



