다음 포스팅은 https://youtu.be/iyySQFfDBMM 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
함수의 역원 (역함수)에 대해서 살펴보기 전에, 다음의 예시를 군의 관점에서 살펴봅시다.
우리가 아는 군의 예시:
㉮. 덧셈을 연산으로 갖는 정수의 모임
㉯. 곱셈을 연산으로 갖는 0이 아닌 유리수의 모임
㉮ 번의 집합을 $Z$ (정수집합을 표현하는 기호)
㉯ 번의 집합을 $Q$-{0}로 표기하자. ($Q$는 유리수 집합을 표현하는 기호)
만약에 $Z$를 정의역으로, $\mathbb{Q}-{0}$을 공역으로 갖는 함수
$f: \mathbb{Z} \longrightarrow\mathbb{Q}$-{0}를 만들고자 (정의하고자) 한다면,
기왕이면 $Z$와 $\mathbb{Q}-${0} 두 집합이 갖고 있는 군 구조와 어울리는 함수를 만들고자 하는게 여러모로 유익할 것이다.
여기서, 어울린다는 의미는 다음을 뜻한다:
함수 $f: \mathbb{Z} \longrightarrow\mathbb{Q}$-{0} 중에서 임의의 두 원소
$x, y \in \mathbb{Z}$ 에 대하여
$
f(x+y)=f(x) \times f(y) \circ\circ\circ(*)
$
를 만족하는 함수를 고려하자.
$*$의 의미 설명
step1 $x, y \in \mathbb{Z}$ 이면 $\mathbb{Z}$는 덧셈을 기준으로 군이므로
$x+y \in \mathbb{Z}$이어야 한다.
step2 $x+y \in \mathbb{Z}$이므로 함수 $f: \mathbb{Z} \longrightarrow\mathbb{Q}-${0}에 의해
$f(x+y)$는 $\mathbb{Q}-${0}의 두 원소이다.
step3 step 1,2 를 잠시 잊어버리고, 이미 선책된 $\mathbb{Z}$의 두 원소 $x, y \in \mathbb{Z}$에 대해 함수 $f: \mathbb{Z} \longrightarrow\mathbb{Q}$-{0}의 두 원소여야 한다.
step4 $\mathbb{Q}-${0}는 곱셈을 기준으로 군이므로 step3의 $f(x), f(y) \in Q-{0}$ 의 곱셈에 의해 $f(x)×f(y)$는
$\mathbb{Q}-${0}의 원소여야 한다.
step5 step 1,2는 정의역에서 연산을 한 후에 함수값을 취한 것이다. 반면에 step3,4는 정의역의 두 원소들을 함수값으로 바꾼후에 공역에서 연산을 한 것이다. 연산 순서가 다르지만, 결과는 같다. 즉, 함수가 연산을 "보존" 한다.
$*$에 대한 관찰들
1. $f(1)=a$라 적자. 양의 정수 $n$에 대해서 $x,n,y=1$로 놓으면, $*$에 의해
$f(n+1) \stackrel{(*)}{=} f(n) f(1) \stackrel{f(1)=a}{=}$ a $f(n)$ 이다 $\circ\circ\circ(A)$
그런데 $x=n-1, y=1$로 다시 놓으면 $*$에 의해
$f(n-1+1) \stackrel{(*)}{=} f(n-1) f(1) \stackrel{f(1)=a}{=} a f(n-1) 이다 \circ\circ\circ(B)$
(A) 와 $(B)$ 를 합치면
$f(n+1) \stackrel{(A)}{=} a f(n)$
$
\begin{aligned}
& \text { (B) } a \times a f(n-1) \\
& =a^{2} f(n-1) .
\end{aligned}
$
이런 식으로 계속 반복하면 다음을 얻는다.
$
\begin{aligned}
f(n) & =a f(n-1)=a^{2} f(n-2)=a^{3} f(n-3) \\
& =\infty=a^{n-1} f(1)=a^{n} .
\end{aligned}
$
즉 양의 정수 (or 자연수) $x$에 대해 $f(x)=a^x$가 된다.
2. $x=y=0$으로 선책하고 $*$를 적용하면
$
f(0+0)=f(0) \times f(0)
$
$
f^{}(0)=f^{}(0)^{2}
$ 이다
이 식을 만족하는 $f(0)$은 오직 0과 1 뿐이다.
$
\begin{aligned}
& \text { 5. } x=f(0), x=x^{2} \Leftrightarrow x-x^{2}=0 \\
& \Leftrightarrow x(1-x)=0 \Leftrightarrow x=0 \text { or } 1
\end{aligned}
$
그런데 $f: \mathbb{Z} \longrightarrow\mathbb{Q} $-\{0\}의 공역에서 0이 배제되어 있으므로 $f(0)$은 반드시 1이어야 한다.
그러므로, $f(0)=1$이다. (즉 $a^0=1$)
의미 임의의
$x,y∈\mathbb{Z}$에 대해서 $f(x+y){=} f(x) \times f(-x)$를 만족하는 함수
$f: \mathbb{Z} \longrightarrow\mathbb{Q}$-{0}는 정의역인 정수집합의
덧셈에 대한 항등원 O $(n+O=O+n=n)$
곱셈에 대한 항등원 1 $(m×1=1×m=m)$으로 대응시킨다.
즉 지수함수는 정의역의 항등원을 공역의 항등원으로 대응시킨다.
3. 임의의 정수 $x$에 대해

즉 $f(x) f(-x)=1$ 이다. $\left ( a^{x} \cdot a^{-x}=1 \stackrel{(2)}{=} a^{0}\right)$
이 식은 $f(x)$와 $f(-x)$가 서로 곱셈의 역원이 됨을 뜻한다. $(a*x=x*a=e)$
의미 $x$와 $-x$는 정의역인 정수 집합에서 덧셈에 대해 서로 역원 관계이다. 이를 $f(x+y){=} f(x) \times f(y)$를
만족하는 함수: $f: \mathbb{Z} \longrightarrow\mathbb{Q}$-{0}는
$f(x)$와 $f(-x)$가 공역인 0이 아닌 유리수 집합에서 곱셈에 대한 역원이 되도록 대응시킨다.
결론 임의의 $x,y∈\mathbb{Z}$에 대해 $f(x+y){=} f(x) f(y)$를
만족시키는 함수 $f: \mathbb{Z} \longrightarrow\mathbb{Q}$-{0}는
- 정의역의 연산을 공역의 연산으로 "보존"하고
- 정의역의 항등원을 공역의 항등원으로 대응시키고 2)설명
- 정의역의 역원을 공역의 역원으로 대응시킨다. 3)설명
이러한 특징을 만족하는 함수 $f(x)=a^x$를 우리는 지수함수라 부른다.
그리고 $f(x)=a^x$의 역함수를 로그함수라 부릅니다. (이제부터 할 이야기 입니다.)
함수의 합성 $\circ$에 대한 역원은 역함수이다
원하는 것은 함수 $f: A \longrightarrow A$가 주어졌을 때,$f\circ{g}=g\circ{f}=\mathbb{I_A}$를
만족하는 $g: A \longrightarrow A$를 찾는 것입니다.
$a*x=x*a=e$에 대응
이 상황을 그림으로 그려보면 다음과 같습니다.

즉 $g$는 $f(a)$를 $a$로 되돌리는 역할을 한다.
이러한 $g: A \longrightarrow A$를 함수 $f: A \longrightarrow A$의 역함수
(inverse function)이라고 부른다. 그런데 이러한 역함수는 언제나 존재하는게 아니며, 함수가 전단사 함수여야만 한다.
정의 함수 $f: A \longrightarrow B$ 가 주어져 있을 때, (줄여서 함수 $f$)
1. 만약에 $x_1, x_2$는 $A$의 원소들이고 $x_1≠x_2$이면 두 함수값 $x_1≠x_2$이면, $f$를 단사 (one to one) 함수라 부른다.)
(대우명제: $f(x1)=f(x2)$이면 $x1=x2$이다)
2. 만약에 공역 (codomain)과 치역(range)가 일치한다면, 다시 말해서, $B$의 임의의 원소 $y$에 대해서 $A$의 원소 $x$
가 존재하여 $y=f(x)$가 될때, $f$를 전사 (onto) 함수라 부른다.
3. 함수가 단사 함수인 동시에 전사함수 이며 전단사 함수 (one to one onto)라고 부른다.
예시

전단사 함수에 대해 이야기하기 전에, 단사함수와 전사함수에 대해 좀 더 살펴보기로 하자
단사함수에 대하여 함수 $f: A \longrightarrow B$에 대하여 함수가 단사함수라고 가정하자. 가령 이런 그림을 생각하는 것이다.

함수가 단사함수이므로, 적어도 $x1≠x2$이면 그의 대응하는 두 함수값 $f(x1)≠f(x2)$임이 보장된다. 따라서 우리는 $f(x)$를 $x$로 유일하게 대응시킬 수 있으므로, B에서 A로 대응하는 함수를 다음과 같이 정의할 수 있다: A에서 아무 원소 $x_0$를 하나 고르자.
함수 $g: B \longrightarrow A$를 정의하되
$y$가 $f: A \longrightarrow B$의 치역의 원소인 경우, $y=f(x)$가 되는 $x∈A$가 존재하므로 $g(y)$sms $x$로 정의하고,
$y$가 $f: A \longrightarrow B$ 치역에 속하지 않는다면 $g(y)=x_0$(아까고른)로 정의한다.
다시 말해, $g: A \longrightarrow B$
$ y \longrightarrow x$ 만약에 $y=(fx)$인 $x∈A$가 있다면
$x_0$ 만약에 $y=(fx)$인 $x∈A$가 존재하지 않다면
여기서 $g: B \longrightarrow A$가 잘 정의되는 이유는 $g: A \longrightarrow B$가 단사함수이기 때문으로, $y$가 $f(x)$로 표현할 때
$x$가 유일함을 보장해주기 때문이다. (만약에 $y$가 $f(x)$이외에 $f(x')$으로도 표현되면 $x=x'$이어야 한다, 그렇지 않으면 $(x1≠x1)$ $f(x)≠f(x')$이어야 하므로 $f: A \longrightarrow B$가 단수함수라는 가정에 모순
우리가 정의한 $g: B \longrightarrow A$는 다음을 만족한다:
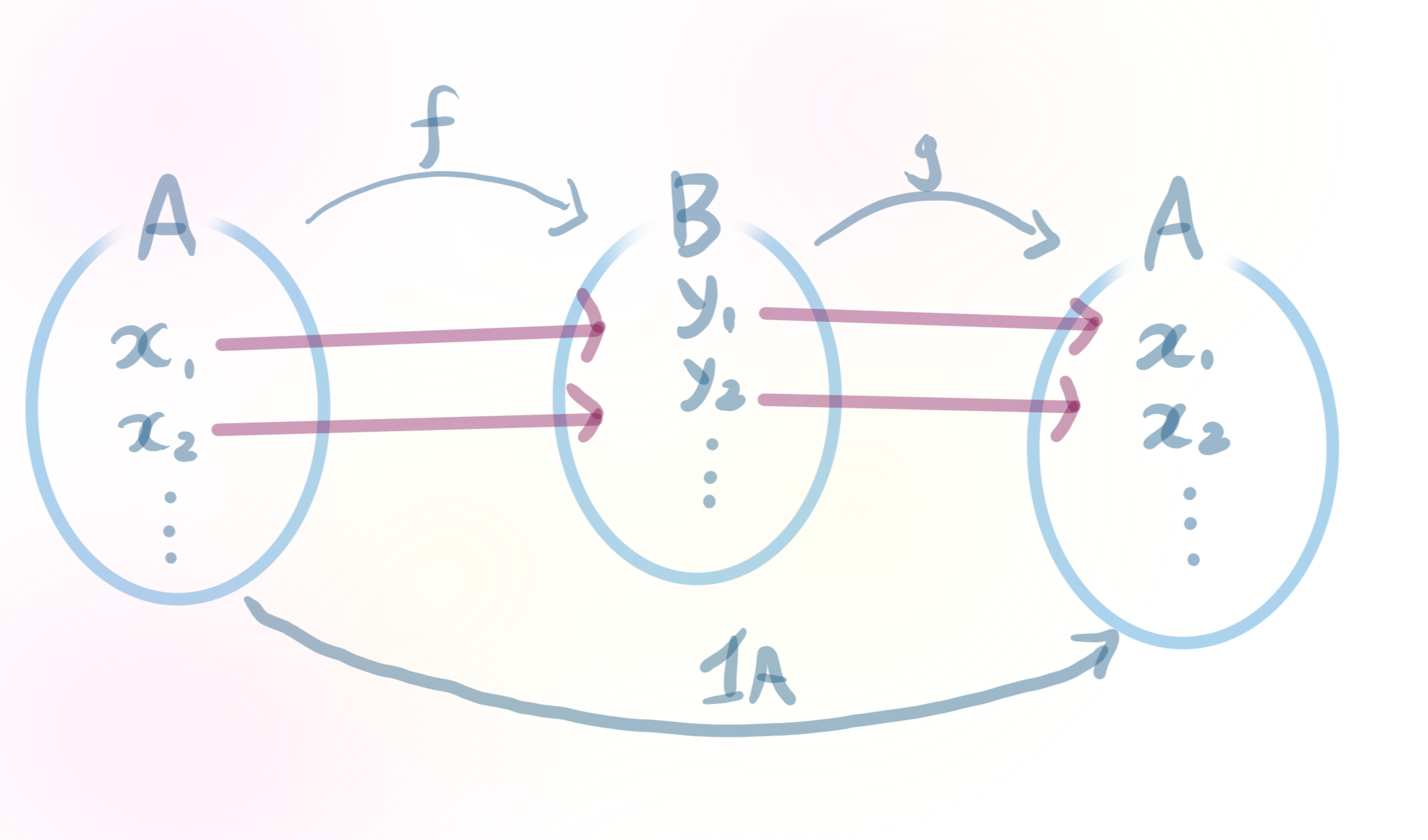
즉, $g \circ f=I_{A}: A \longrightarrow$ A 이다.
연습문제 위의 논지의 역 (converse)를 보여라.
다시 말해서, 함수 $f: A \longrightarrow B$에 대해 또 다른 함수 $g: B \longrightarrow A$가 존재하여 $g \circ f=I_{A}: A \longrightarrow$ A이면 $f$는 반드시 단사함수이다.
사실, 우리는 지금까지 다음을 이야기한 것이다:
명제1 함수 $f: A \longrightarrow B$가 주어질때 다음의 두 문장은 동치이다:
(A) 함수 $f: A \longrightarrow B$는 단사함수이다.
(B) $g \circ f=I_{A}: A \longrightarrow$ A가 되는 함수 $g: B\ longtightarrow$A가 존재한다.
(A) → (B): 위에서 보임
(B) → (A): 위의 연습문제
이번에는 전사함수에 대해서도 살펴보자.
전사함수에 대하여 함수 $f:A\longrightarrow$ B가 전사함수라고 가정하자.
가정에 의해 b의 임의의 원소 $y$에 대해 $f(x)$로 표현되는 $x$가 적어도 하나 존재한다. (그러나, '하나'만 있어야 하는 것은 아니다)
(이하의 논의는 참이지만, 커다란 구멍이 존재합니다. 생각해보세요)
역시 함수 $g: B \longrightarrow A$를 정의하되, B의 임의의 원소 $y$를 선택하고 $y=f(x)$로 표현되는 $x$에 대해 $g(y)=x$로 정의하자. 마치,

그러면, $g: B \longrightarrow A$는 $f\circ{g}=I_B$를 만족한다.
관찰 위의 $g: B \longrightarrow A$가 정말로 장 정의된다고 말할 수 있나요?
그렇지 않습니다.
왜냐하면 B의 각 원소 $y$마다 $f(x)$로 표현되는 $x$는 존재하지만 유일하리란 보장은 없기 때문입니다.
즉 각 $y∈B$마다 $y=f(x)$로 표현되는 $x∈B$를 선택해서 $y$를 이 $x$로 대응시키는 방식으로 $g$를 정의하자고 할 것입니다.
물론 집합 B가 유한집합이면 각 $y$마다 $x$를 계속 선택해나가면 아무 문제가 없습니다.
그런데 만일 B가 무한집합이라면? $y$마다 $x$를 일일히 선택할수 있다고 말하기에 애매해집니다. 즉 이 또한 무한집합을 다루기 위한 '공리'의 영역에 해당하게 되는 것입니다. 이러한 선택이 가능하다고 받아들이는 것을
선택공리 (axiom of choice)라고 부릅니다.
코멘트 선택공리를 받아들이지 않는 수학자들도 있습니다.
연습문제 위의 논지의 역 (Converse)를 보여라.
다시 말해서, 함수 $f: A \longrightarrow B$에 대해 또다른 함수 $g: B \longrightarrow A$가 존재하여
$f \circ g=I_{B}:B \longrightarrow$B이면 $f$는 반드시 전사함수이다.
사실은, 우리는 지금까지 다음을 이야기한 것이다:
명제2 함수 $f: A \longrightarrow $B가 주어질때 다음의 두 문장은 동치이다:
(A) 함수 $f: A \longrightarrow$B는 전사함수 이다.
(B) $f \circ g=I_{B}:B \longrightarrow$B가 되는 함수 $g:B \longrightarrow$A
(A) → (B): 선택공리
(B) → (A): 위의 연습문제
연습문제
1) 두 함수 $f: A \longrightarrow B$, $g: B \longrightarrow C$가 모두 단사함수이면 $g \circ f:A \longrightarrow$C도 단사함수임을 보여라.
2) 두 함수 $f: A \longrightarrow B$, $g: B \longrightarrow C$가 모두 전사함수 이면 $g \circ f:A \longrightarrow$C도 전사함수임을 보여라.
3) 만약에 두 함수 $f: A \longrightarrow B$, $g:B \longrightarrow$C의 합성함수 $g \circ f:A \longrightarrow$C가 단사함수이면 $f$도 단사함수임을 보여라.
4) 만약에 두 함수 $f: A \longrightarrow B$, $g:B \longrightarrow$C의 합성함수 $g \circ f:A \longrightarrow$C가 전사함수이면 $g$도 전사함수임을 보여라.
다음시간! 선형함수, 행렬, 다항함수
'직장인과 문과생을 위한 수학교실 (직문수)' 카테고리의 다른 글
| 6강. 역행렬과 행렬식의 의미, 선형대수학 Part B (0) | 2023.08.03 |
|---|---|
| 5강. 벡터공간과 행렬, 선형대수학 Part 1 (0) | 2023.08.02 |
| 3강. 함수의 정의와 군 (0) | 2023.08.01 |
| 2강. 근의 공식과 대수학, 자연수 집합의 페아노공리계와 군의 정의 (0) | 2023.07.31 |
| 1강. 집합과 공리 (0) | 2023.07.30 |



