다음 포스팅은 https://youtu.be/SR4-KBe8vhQ 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
지난시간
- 행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ 는 선형함수 $
\begin{aligned}
& f: \mathbb{R} \rightarrow \mathbb{R}^{2}, f\left(\left(\begin{array}{l}
x \\
y
\end{array}\right)\right)=\left(\begin{array}{l}
a b \\
c d
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right) \\
\end{aligned}$에 대응되며, 역함수 $f^-1$가 존재할 필요충분조건은 선형함수 $f^-1$에 대응하는 행렬 $A^{-1}=\frac{1}{a d-b c}\left(\begin{array}{cc}d & -b \\ -c & a\end{array}\right)$가 존재하는 여하와 같고, 이는 행렬식 (determinant) det(A)=$ab-bc$가 0이 아닌 여하와 같다. - 행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$의 행렬식 $ad-bc$는 두 벡터 $(a,b),(c,d)∈\mathbb{R^{2}}$가 형성하는 평행사변형의 면적과 일피한다고 주장했다.
- 수학적 대상들을 하나하나 살펴보면서 등장하기 시작한 관점들
- 공리주의적 관점 → 군의 관점 → 기하학적 관점, 같은 대상, 여러 해석.
- '해석'이외에 우리가 진짜로 할 수 있는것: 숫자의 덧셈과 곱셈
이 렉처의 목적 위주장을 이해하는 과정에서 선형대수학과 기하학의 본질적인 관계에 대해 살펴볼 기화를 갖는것.
기하학이란? Geometry-Geometria(Latin); "Measurement"
구조를 갖고있는 집합을 '공간'으로 바라볼때, 이 공간을 이해하는데 유익한 구체적인 '양'과 그 함의를 공부하는 수학
ex)'도형'이라 불렀던 집합의 길이, 각도, 넓이, 부피...
삼각함수 (Trigonometric Functions)

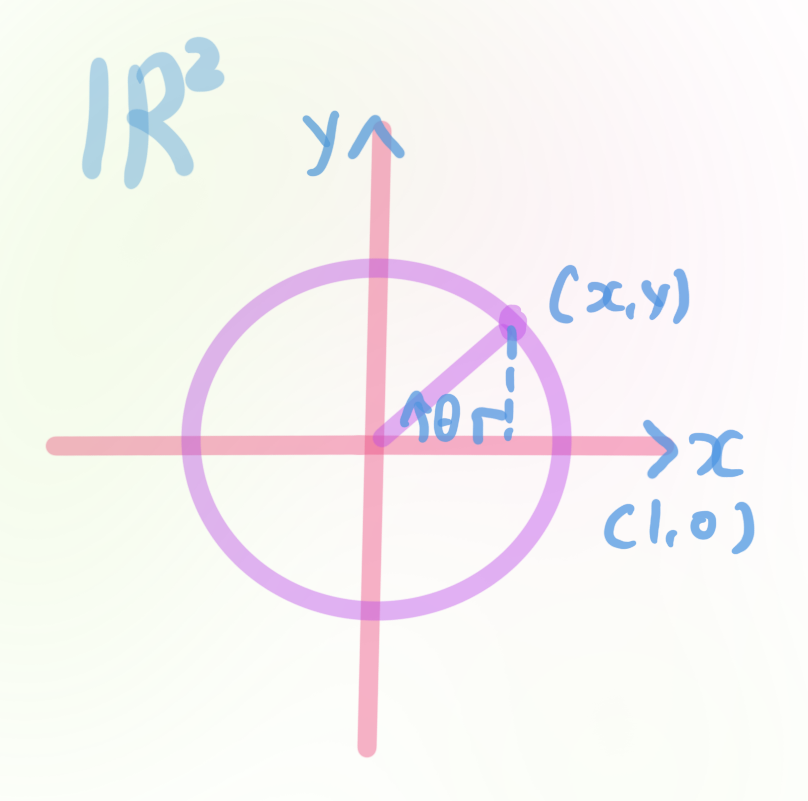
집합 $\mathbb{R}$에서 각도로 결정되는 함수들을 삼각함수라 한다.
반지름의 크기가 1이고 원점을 중심으로 갖는 원을 생각하자.
원 위의 모든 점 $(x,y)$는
밑변이 $x$, 높이가 $y$, 빗변이 1인 직각삼각형을 형성하므로, 피타고라스의 정리에 의하여 $x^2+y^2=1^2=1$을 만족한다.
그런데, 사실 원 위의 모든 점 $(x,y)$는 $x$축에서 반시계 방향으로 $\theta$만큼 (1,0)을 회전시키면 얻을 수 있다.
즉 $x$와 $y$는 각각
$\theta$에 대해 함수가 되는 것이다. 그러므로 우리는 $x$를 코사인 함수

$x=cos\theta$로 부르고, $y$를 사인함수 $y=sin\theta$로 정의한다.
정의에 의해서 임의이 각도 $\theta$에 대해 $(cos\theta)^{2}+(sin\theta)^{2}=1$이다.
정의
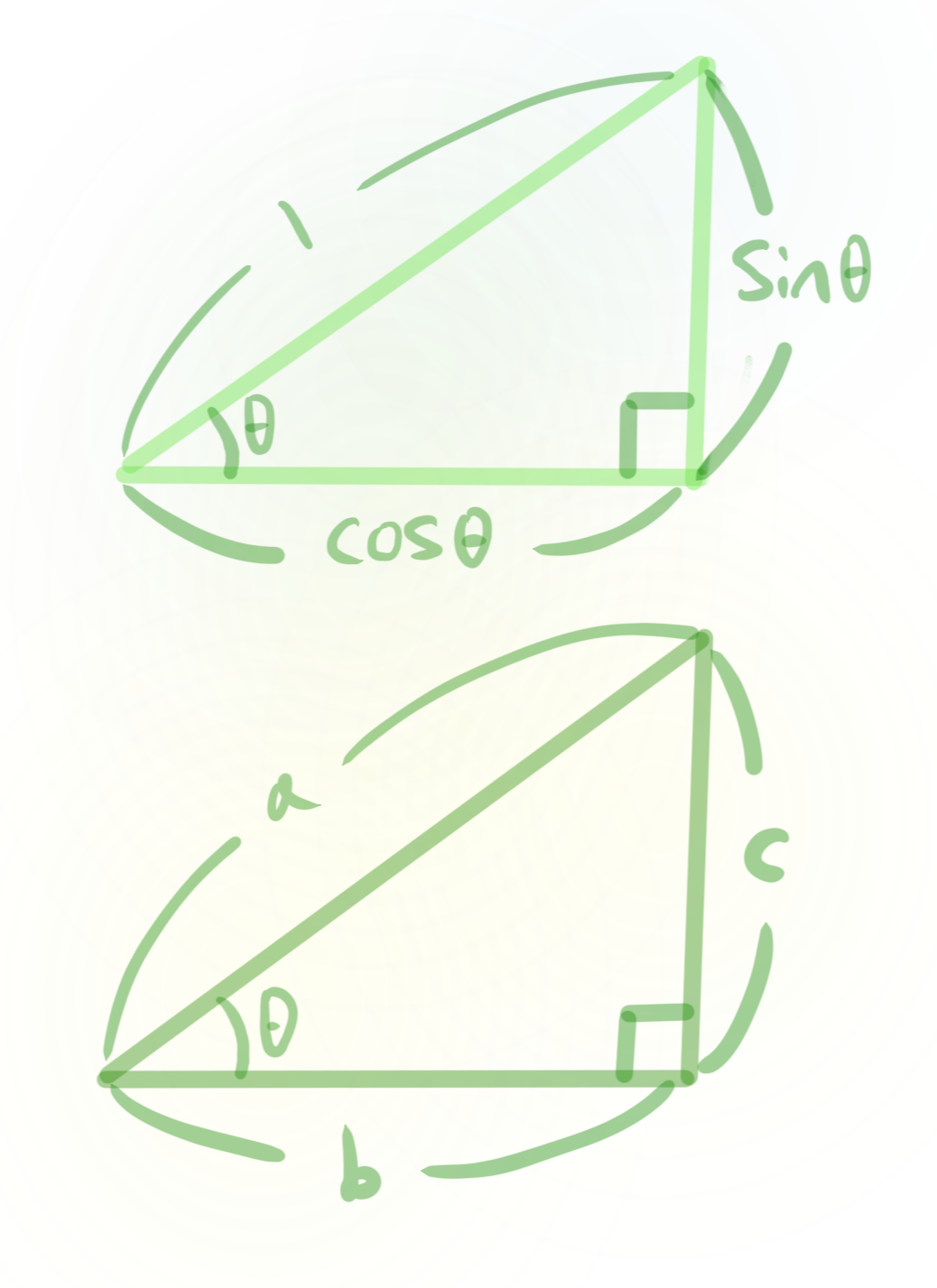
- 빗변의 크기가 1인 직각삼각형에 대해서 빗변과 밑변의 사잇각이 $\theta$일때, 밑변을 $cos\theta$, 높이를 $sin\theta$로 정의한다.
- 더 일반적으로, 빗변, 밑변, 높이의 크기가 각각 $(a,b,c)$인 직각삼각형에 대해서, $sin\theta=\frac{a}c, cos\theta=\frac{b}a$로 정의한다 ($a=1$이면 위의 정의와 같아진다.)
회전행렬 벡터공간 $\mathbb{R^{2}}$위에서 반지름이 1이고 중심이 원점인 원을 생각하자. 회전시키고자 하는 양인 $\theta$를 고정하고, 두 벡터 (1,0)과 (0,1)을 각각 반시계 방향으로 $\theta$만큼 회전시키자.

연습문제 (1,0)을 \$theta$만큼 회전하면 $(-sin\theta,cos\theta)$,(0,1)을 $\theta$만큼 회전하하면 $(-sin\theta,cos\theta)$가 되는 것을 위의 삼각함수들의 정의만을 사용하여 확인해보세요.
우리는 선형함수 $
\begin{aligned}
& f: \mathbb{R} \rightarrow \mathbb{R}^{2}, f\left(\left(\begin{array}{l}
x \\
y
\end{array}\right)\right)=\left(\begin{array}{l}
a b \\
c d
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right) \\
\end{aligned}$중에서 벡터 $(x,y)$를 반시계 방향으로 $\theta$만큼 회전시키는 그러한 $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$를 찾고 싶다. (이를 '회전행렬' (rotation matrix)라고 부릅니다.)
위의 그림 및 연습문제로 부터,

이다. 즉, $a=cos\theta$, c=sin\theta, b\-sin\theta, d=cos\theta$이다.
즉, $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right)$ 를 얻는다.
정리하면, $
\left(\begin{array}{ll}
cos\theta & -sin\theta \\
sin\theta & cos\theta
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)
$는 벡터 $\left(\begin{array}{l}x \\y\end{array}\right)$ $(or (x,y))$를 반시계 방향으로 $\theta$만큼 회전시켜주는 선형함수 이다.
명제 $(ad-bc)$는 두 벡터 $(a,b)$와 $(c,d)$가 만드는 평행사변형의 면적이다.

확인 다음과 같은 그림을 생각하자:
벡터 $(a,b)$가 빗변이 되는 직각삼각형 에서 빗변과 밑변의 사잇각을 $\theta$라 하자.

면적을 계산하기 위해 평행사변형을 시계방향으로 $-\theta$만큼 (즉 반시계 방향으로 $-\theta$만큼) 회전행렬을 사용하여 회전시키자.

평행사변형의 면적은 회전하더라도 바뀌지 않아야 할 것이다.
회전한 평행사변형의 면적은 빗금친 삼각형의 넓이 $1\frac1{2}a'b'$의 2배이다. 즉 $2 \times \frac{1}{2} \times a^{\prime} d^{\prime}=a^{\prime} d^{\prime}$ 그런데 회전행렬 및
$cos(-\theta)=cos\theta,sin(-\theta)=-sin\theta$임을 사용하면 (아래노트 참조)
$
\begin{aligned}
& \left(\begin{array}{l}
a^{\prime} \\
b^{\prime}
\end{array}\right)=\left(\begin{array}{ll}
\cos (-\theta) & -\sin (-\theta) \\
\sin (-\theta) & \cos (-\theta)
\end{array}\right)\left(\begin{array}{l}
a \\
b
\end{array}\right)=\left(\begin{array}{c}
a \cos \theta+b \sin \theta \\
-a \sin \theta+b \cos \theta
\end{array}\right) \\
& \left(\begin{array}{l}
c^{\prime} \\
d^{\prime}
\end{array}\right)=\left(\begin{array}{cc}
\cos (-\theta) & -\sin (-\theta) \\
\sin (-\theta) & \cos (-\theta)
\end{array}\right)\left(\begin{array}{l}
c \\
d
\end{array}\right)=\left(\begin{array}{c}
c \cos \theta+d \sin \theta \\
-\operatorname{csin} \theta+d \cos \theta
\end{array}\right)
\end{aligned}
$이고,
graphic 로부터 $\sin \theta=\frac{b}{\sqrt{a^{2}+b^{2}}}, \cos \theta=\frac{a}{\sqrt{a^{2}+b^{2}}}$이다. 이들을 사용해서 $(a',d')$를 계산하면
$
\begin{aligned}
& a^{\prime} d^{\prime}=(a \cos \theta+b \sin \theta)(-\operatorname{csin} \theta+d \cos \theta) \\
& =-a c \cos \theta \sin \theta+a d(\cos \theta)^{2}-b(\sin \theta)^{2} \\
& +b d \sin \theta \cos \theta \\
& =-a c \frac{a b}{a^{2}+b^{2}}+a d \frac{a^{2}}{a^{2}+b^{2}}-b c \frac{b^{2}}{a^{2}+b^{2}}+b d \frac{a b}{a^{2}+b^{2}} \\
& =\frac{1}{a^{2}+b^{2}}\left(-a^{2} b c+a^{3} d-b^{3} c+a b^{2} d\right) \\
& =\frac{1}{a^{2}+b^{2}} \times\left(a^{2}+b^{2}\right)(a d-b c) \\
&=ad-bc
\end{aligned}
$ 그러므로 평행사변형의 면적은 ad-bc이다. Q.E.D
노트

$\cos \theta=\cos (-\theta)$
$\sin (-\theta)=-\sin \theta$
별거 아닌거 같지만 너무너무너무너무너무 중요한 전제에 대한 질문
우리는 '각도'로 부터 삼각함수들을 정의했고, 삼각함수로부터 회전행렬을 정의하여 벡터를 회전시킨다는 생각을 할 수 있었다.
여기서 각도는 두 벡터가 이루는 관계를 표현하는 양이다.
질문입니다. 각도란 그래서 정확히 무엇입니까?
이어서, 우리는 이미 벡터의 크기를 평행사변형을 이루는 변의 크기로 위에서 사용했습니다. 벡터의 크기는 말 그대로 각 벡터가 갖는 고유의 값입니다.
두 번째 질문입니다. 그래서 벡터의 크기란 정확히 무엇입니까?
너무 당연한 것을 묻는 것처럼 느껴지시나요? 가령 다음을 생각해 봅시다.
우리는 행렬 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$이 만약에 $ad-bc≠0$을 만족한다면 이는 선형함수 $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$가 전단사 함수를 의미하는 것임을 알고 있습니다. (6번째 렉쳐)
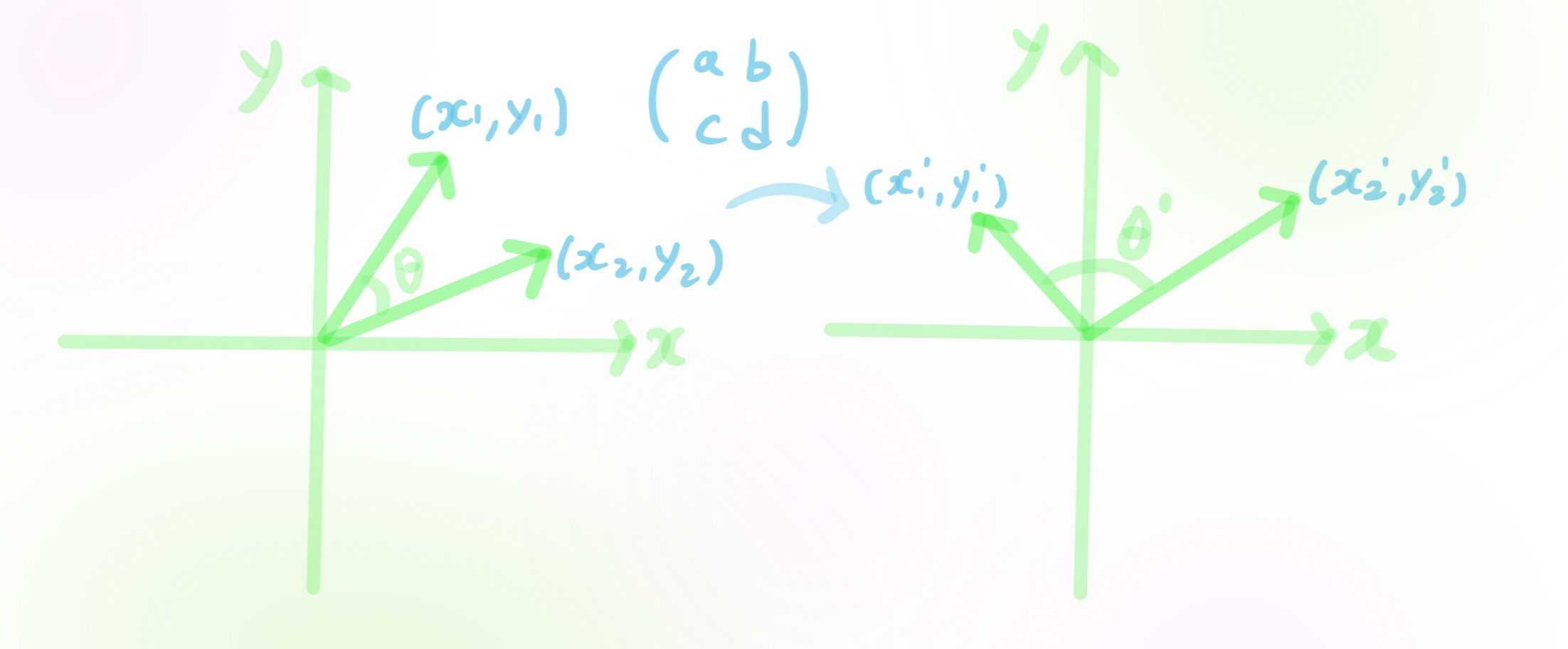
왼쪽 그림에서 두 벡터간의 각도 및 한 벡터의 크기는, 오른쪽 그림으로 벡터들을 옮겨주면 해당값들은 당연히 달라집니다.
그러면 좌우 그림 중에 어디를 기준으로 값을 잴지 정해주면 되는거 아니냐고 반문하실 수도 있습니다. 그렇습니다. 이 기준을 정해주면 됩니다. 선형대수학 (linear algebra) 에서는 각도와 크기를 정해주는 수학적 기준을 내적 (inner product)이라고 부릅니다.
원하는 것:
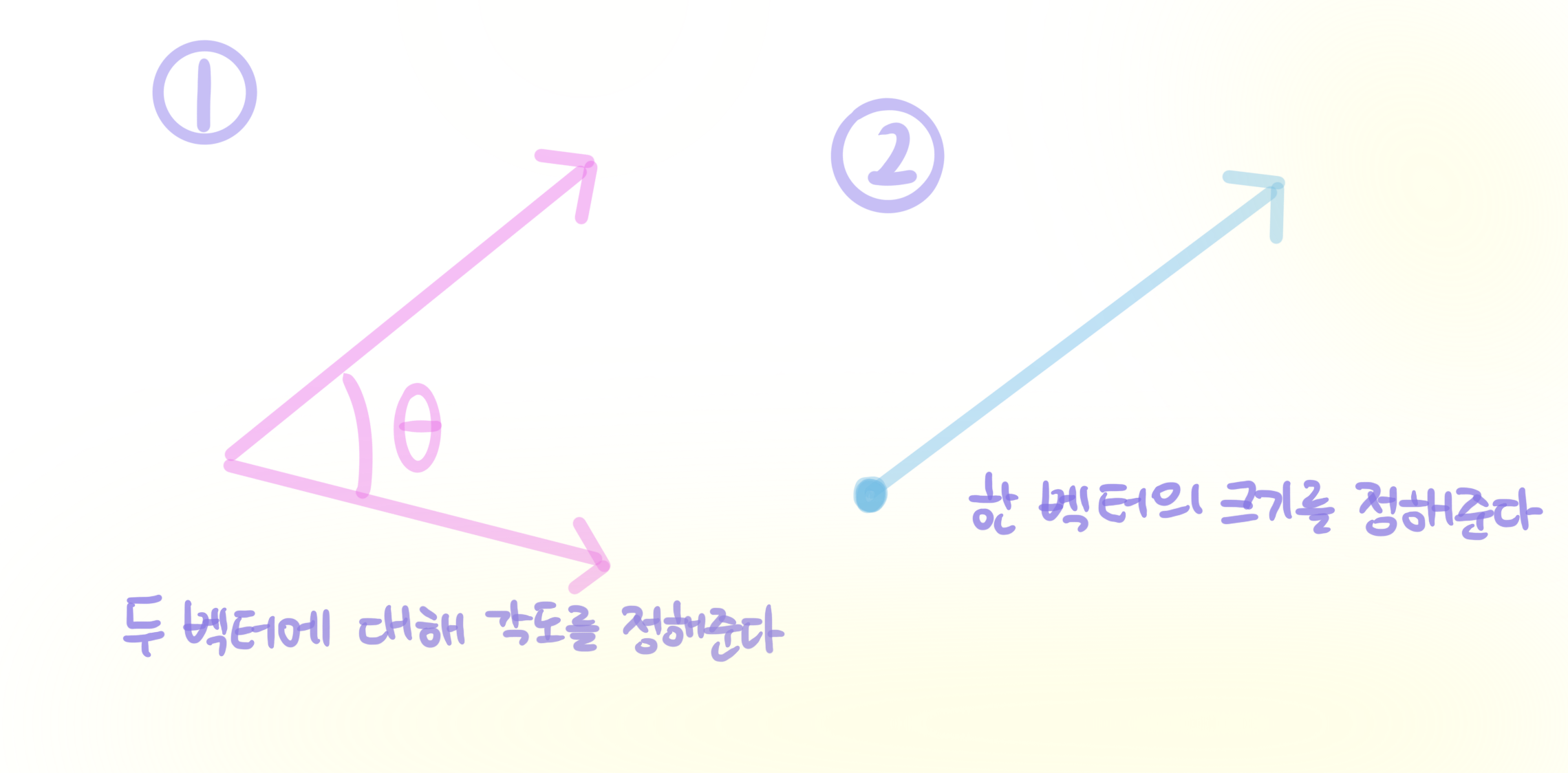
두 벡터에 대해 각도를 정해준다
정의 벡터공간 $\mathbb{R}^{2}=\{(x, y) \mid x, y \in \mathbb{R}\}$에 대해서
내적은 $\langle\cdot, \cdot\rangle: \mathbb{R}^{2} \times \mathbb{R}^{2} \longrightarrow \mathbb{R}$
$((a, b),(c, d)) \longrightarrow\langle(a, b),(c, d)\rangle$
은 두 벡터를 받아서 실수값을 출력해주는 함수 중에서 아래의 조건들을 모두 만족할때 내적이라 부른다:
- 임의의 벡터 $(a,b)$∈$\mathbb{R}^{2}$에 대해서
$\begin{aligned}& \langle(a, b), \cdot\rangle: \mathbb{R}^{2} \longrightarrow \mathbb{R} \\& (c, d) \mid \longrightarrow\left\langle(a, b),\left(c_{1} d\right)\right\rangle\end{aligned}$ 는 성형함수이다. 즉 $
\begin{aligned}
& \left(\left\langle(a, b),\left(c_{1}, d_{1}\right)+\left(c_{2}, d_{2}\right)\right\rangle\right. \\
& =\left\langle(a, b),\left(c_{1}, d\right)\right\rangle+\left\langle(a, b),\left(c_{2}, d_{2}\right)\right\rangle \\
& \langle(a, b), K \cdot(c, d)\rangle=K\langle(a, b),(c, d)\rangle)
\end{aligned}
$ - 임의의 두 벡터 $(a,b),(c,d)$에 대하여 $\langle(a, b),(C, d)\rangle=\langle(c, d),(a, b)\rangle\$이다.
- 임의의 벡터 $(a,b)$에 대해 $\langle(a, b),(a, b)\rangle$는 항상 0보다 크거나 같으며 0이 될 때는 오직 $(a,b)=(00)$일 때이다.
- 내적 $\langle\cdot,\cdot\langle$이 주어질때, 우리는 임의의 벡터 $(a,b)$의 크기를 $\sqrt{\langle(a, b),(a, b)\rangle}$으로 정의하고 $||(a,b)||$로 표기한다.
- 내적 $\langle\cdot,\cdot\langle$이 주어질 때, 우리는 임의의 두 벡터 $(a,b)$, $(c,d)$의 사잇각 $\theta$의 코사인 함수 $cos\theta$를 다음의 관계식으로 정의한다:
$\langle(a, b),(c, d)\rangle=\|(a, b)\| \cdot\|(c, d)\| \cos \theta$
식의 의미:

내적 <$\cdot$>에 대하여
- 임의의 두 벡터 $(a,b),(c,d)$에 대해 $
\begin{aligned}
&\langle(a, b),(c, d)\rangle \\
&=\langle(a, b), c \cdot(1,0)+d \cdot(0,1)\rangle \\
&=c \cdot\langle(a, b), c 1,0)\rangle+d \cdot\langle(a, b),(0,1)\rangle \\
&= c \cdot\langle(1,0),(a, b)\rangle+d \cdot\langle(0,1),(a, b)\rangle \\
&= c \cdot\langle(1,0), a \cdot(1,0)+b \cdot(0,1)\rangle+d\langle(0,1), a \cdot(1,0)+b(0,1)\rangle
\end{aligned}
$
$
\begin{aligned}
& =c \cdot(a \cdot\langle(1,0),(1,0)\rangle+b \cdot\langle(1,0),(0,1)\rangle) \\
& +d \cdot(a \cdot\langle(0,1),(1,0)\rangle+b \cdot\langle(0,1),(0,1)\rangle) \\
& =\langle(1,0),(1,0)\rangle a c+\langle(1,0),(0,1)\rangle b c \\
& +\langle(0,1),(1,0)\rangle a d+\langle(0,1),(0,1)\rangle b d
\end{aligned}
$ 를 얻는다. 이를 행렬들 간의 곱셈으로 표현하면 아래와 같다:
$
=\left(\begin{array}{ll}
a & b
\end{array}\right)\left(\begin{array}{ll}
\langle(1,0),(1,0)\rangle & \langle(1,0),(0,1)\rangle \\
\langle(0,1),(1,0)\rangle & \langle(0,1),(0,1)\rangle
\end{array}\right)\left(\begin{array}{l}
c \\
d
\end{array}\right)$
기준에 해당하는 내적 <$\cdot,\cdot$>에 의해 결정되는 2×2 행렬.
즉 내적 <$\cdot,\cdot$>을 할당하는 것은 위에 해당하는 행렬을 하나 결정하는 것과 같다.
2. 행렬 $\left(\begin{array}{lll}\langle(1,0),(0,1)\rangle & \langle(1,0),(0,1)\rangle \\ \langle(0,1),(1,0)\rangle & \langle(0,1),(0,1)\rangle\end{array}\right) \text{로}$ $\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$ 로 선택해보기로 하자. 그러면 $\left\langle\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)\right\rangle$
$
\begin{aligned}
& =\left(\begin{array}{ll}
x_{1} & y_{1}
\end{array}\right)\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\left(\begin{array}{l}
x_{2} \\
y_{2}
\end{array}\right) \\
& =\left(\begin{array}{ll}
x_{1} & y_{1}
\end{array}\right)\left(\begin{array}{l}
x_{2} \\
y_{2}
\end{array}\right)=x_{1} x_{2}+y_{1} y_{2}\
\end{aligned}$가 된다.
고등학교 과정에서는 이 내적을 dot product라 부른다. 이 경우에 벡터 $(x,y)$의 크기를 내적의 정의를 토대로 계산해보면
$
\begin{aligned}
\|(x, y)\| & =\sqrt{\langle(x, y),(x, y)\rangle} \\
& =\sqrt{\left(\begin{array}{ll}
x & y
\end{array}\right)\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)} \\
& =\sqrt{\left(\begin{array}{ll}
x & y
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)=\sqrt{x^{2}+y^{2}}}
\end{aligned}
$
이는 우리가 익숙하게 사용해온 피타고라스의 정리이다:
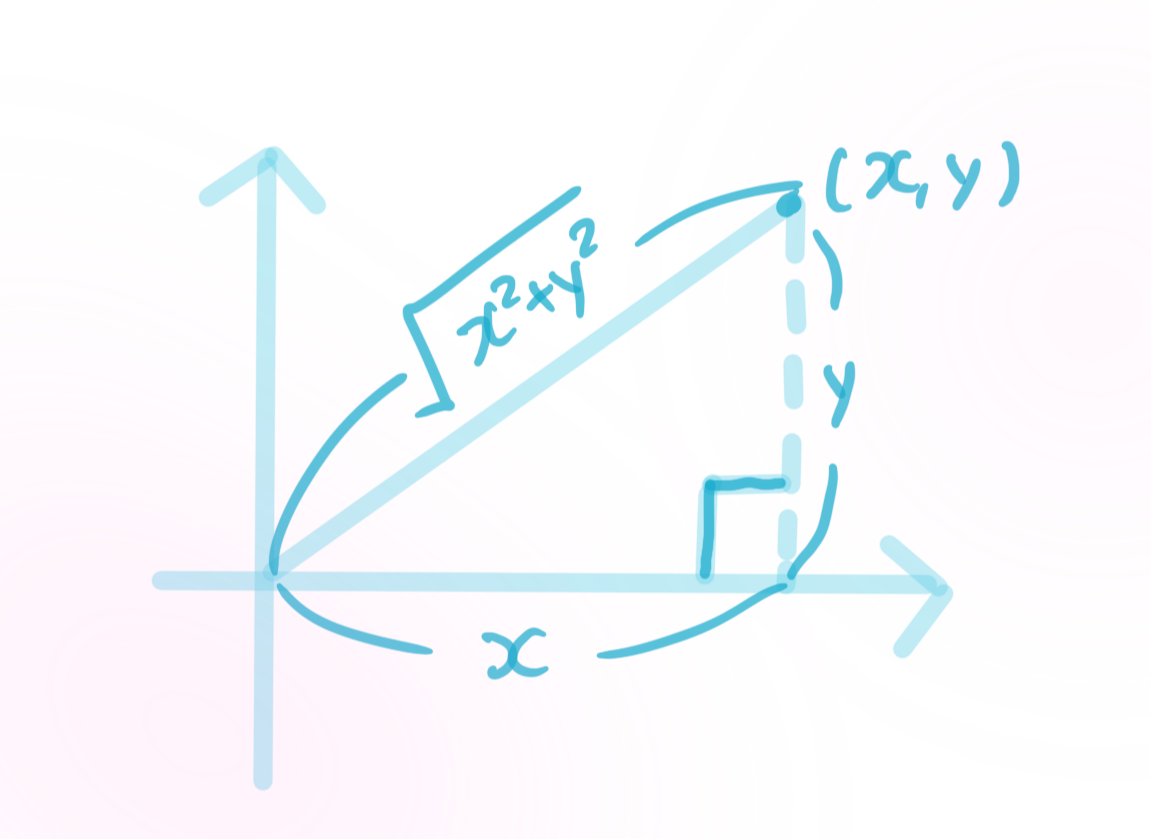
즉 벡터 $(x,y)$의 크기가 $\sqrt{x^{2}+y^{2}}$로 우리가 간주해온 것은 절대적인 진리가 아니라 내적에 해당하는 행렬은 항등행렬로 두었기 때문이다.
내적을 항등행렬로 설정한 기하학을 유클리드 기하학이라 부르고, 그렇지 않은 다른 기하학을 비유클리드 기하학 (or 리만기하학 Riemannian Geometry)이라고 부른다.
3. 내적이 정해지는 순간 각 벡터의 크기와 두 벡터간의 사잇각이 정해진다. 즉, 공간 $\mathbb{R}^{2}$의 벡터들의 구체적인 생김새들이 결정된다. 다시 말해서, 내적은 공간의 기하학적 구조를 완전히 지배한다! 기하학에서는 내적을 리만기하학의 창시자인 베를하르크 리만의 이름을 따서 리만메트릭 (Riemannian Metric)이라 부르고 그의 지도교수인 가우스의 앞글자를 따서 대개 $'g'$로 표기한다.
4. 비유클리드 기하학이 구체적으로 쓰이는 용예는 여러 응용학문들에서 무수히 많습니다. 일례로 통계학에서는 내적에 해당하는 행렬로 피셔정보행렬(Fisher Information Matrix)를 사용합니다.
통계학과 인공지능에서 가장 많이 사용되는 확률분포인 정규분포의 모임은 피셔정보행렬을 내적으로 사용하면 쌍곡기하학 (Hyperbolic Geometry)의 표준 공간이 됩니다. 쌍곡기하학 구조는 우리가 살아가는 시공간의 기하학적 구조이기도 합니다. (상대성 이론)
5. 우주선, 비행기의 항법 (히든피겨스)
휘어져 있는 구면의 각 점마다 접평면 $\mathbb{R}^{2}$위에 적절한 내적을 할당하여 매순간 벡터를 잘 선택하여 결과적으로 최단거리로 이동하게 만든다.

다음 시간 회전행렬, 내적 이어서 계속 이야기
'직장인과 문과생을 위한 수학교실 (직문수)' 카테고리의 다른 글
| 9강. 현대수학에서 미분법의 직관과 의미 (0) | 2023.08.04 |
|---|---|
| 8강. 선형대수학의 꽃, 무지개 정리 (0) | 2023.08.04 |
| 6강. 역행렬과 행렬식의 의미, 선형대수학 Part B (0) | 2023.08.03 |
| 5강. 벡터공간과 행렬, 선형대수학 Part 1 (0) | 2023.08.02 |
| 4강. 군의 관점에서 살펴보는 지수법칙과 역함수 (0) | 2023.08.02 |



