다음 포스팅은 https://youtu.be/xpA6OMdj9vU 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
1. 집합과 명제, 공리
- 수학적인 주장은 언제나 참과 거짓만 취급한다. (이게 정말일까요?)
YES or NO 를 판단하는것; 특정 '집합'에 속하는 여하로 판단하는 것과 같음.
예시) 강아지는 고양이가 아니다.
$\Leftrightarrow$강아지는 고양이의 모임에 속하지 않는다.
$\Leftrightarrow $

추상화 : 강아지 $\Leftrightarrow$ x,
고양이의 모임 $\Leftrightarrow$ S,
$\Leftrightarrow x \notin S$
- X는 원소 (element), S는 집합 (Set)이라 부르고 싶다.
여기서 필요한 질문,
질문) 원소란 무엇인가? 어던 집합에 속한 것

그러면 집합 S란 무엇인가? 어떤 기주을 만족시키는 원소들을 모은 것, 이라고 우리는 수학의 정석에서 배웠습니다.
마치,

라고 하면 다 되는 것처럼. 정말 그러할까요?
가령,
- 이발사 왈, " 자신의 수염을 스스로 자르지 않는 사람들에게만 수염을 잘라주겠다."
→ 기준 정립.
→ 집합 S (이발사가 수염을 깎아주는 이들의 모임)
그러면, 이발사 X는 S의 원소이면서
동시에 S의 원소이면 안된다. 모순
(이를 '이발사의 역설' 이라 부릅니다.)
문제점) 집합을 단순히 원소를 모은 것으로 여겼으므로
→ 집합을 규정하는 과정에서 무언가가 더 필요하다.
여기서 '무언가'를 우리는 공리 (axiom) 이라 부를 것입니다.
공리를 도입하기에 앞서,
본적있는 그림
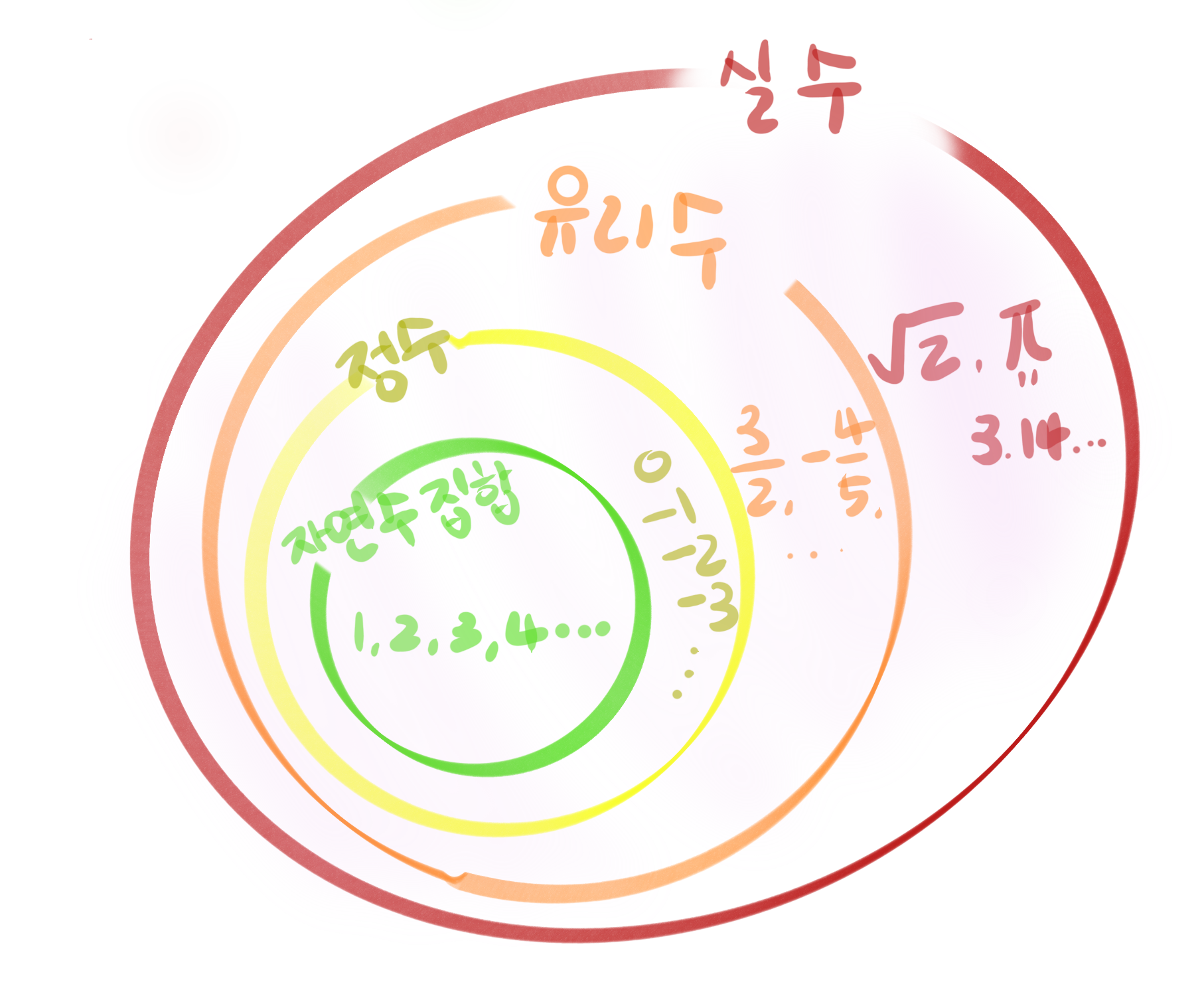
질문들
- 정수의 집합은 자연수 집합보다 크다?
- 유리수의 집합은 정수의 집합보다 크다?
이 모든 질문의 답은 전부 거짓 입니다.
1) 자연수의 집합 ← 일대일 대응 → 정수의 집합
자연수의 집합을 짝수의 모임과 홀수의 모임으로 나누자.
짝수의 경우,
0(=2X0)은 0으로,
2=(2X1)는 1로,
4=(2X2)는 2로,
일반적으로,
2N (=2XN)은 N으로 대응
홀수의 경우,
1(=2X0+1)은 -1로,
3(=2X1+1)은 -2로,
5(=2X2+1)은 -3로,
일반적으로,
2N+1(=2N+1)은 - (N+1)로
즉, 자연수와 정수는 각각 하나씩 전부 대응된다.
그러므로 정수의 모임의 개수와 자연수의 모임의 개수는 일치한다.
(특히, 짝수의 모임, 홀수의 모임, 자연수의 모임이 모두 일대일 대응이 됨 또한 알 수 있다. - 연습문제)
2) 정수의 집합 역시 유리수의 집합과 일대일 대응이 됨을 보이고자 한다.
정수는 양의 정수,0, 음의 정수로 구성되어 있고,
유리수 역시 양의 유리수, 0 ,음의 유리수로 이루어져 있으므로 각각의 0은 서로 대응시키면 되고,
양의 정수 (즉 자연수)와 양의 유리수의 일대일 대응 관계를 찾아내면 음의 경우는 부호만 바꾸어주면 될 것이다.
(이하 논증에는 한가지 논리적 허점이 있습니다, 결과적으로 논증 자체는 참이지만 이를 정확히 메꾸는 과정은 상당한 수고를 요구합니다.
우리는 이 방향으로 가지는 않을 것입니다. 그럼에도 이 허점을 찾아보세요)
모든 양의 유리수는 분수꼴 M/N로 나타낼 수 있으므로
분모가 같은 수들을 다음과 같이 배치하자

양의 정수(자연수)와 일대일 대응 시킨다는 방법을 찾는 것은 양의 유리수를 하나씩 순차적으로 세는 방법을 찾는 것과 같다. 유리수를 하나씩 순차적으로 세는 방법을 찾는 것과 같다. 한 가지 괜찮은 방법으로,
위의 나열된 양의 유리수들을 대각선 방향으로 세면 된다.
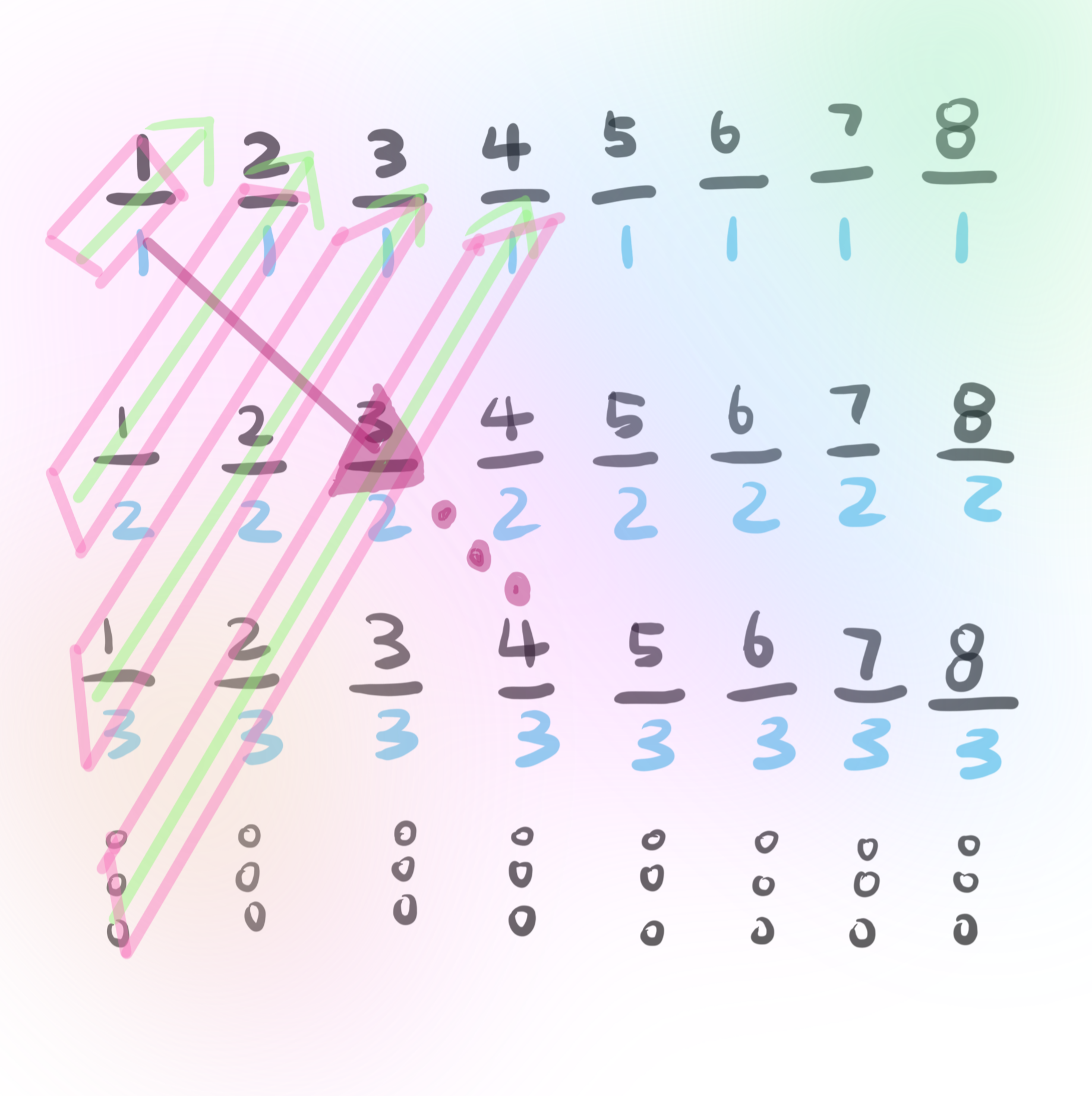
(고등학교 수열 단원에서 이 세는 방법을 '군수열'이라 부릅니다)
양의 유리수를 순차적으로 셀 수 있으므로 양의 정수와 일대일 대응이 성립한다. 그러므로 위의 논의에 의해 정수와 유리수 간의 일대일 대응이 성립한다.
이 시점에서 다시 질문,
3) 유리수와 실수 간에도 일대일 대응이 성립한다.
이 또한 대답은 거짓입니다.
우리는 결론을 부정하여 모순을 이끌어냄으로서 결론이 참임을 보이고다 한다. (이러한 논증을 '귀류법'이라 부릅니다)
만약에 유리수와 실수간에 일대일 대응이 성립한다고 가정하자.
그런데 우리는 이미 확인한 1(.2)로부터 자연수와 유리수 사이에 일대일 대응이 성립함을 알고있다. 그러므로 유리수와 실수이 일대일 대응이 성립하면 자연수와 실수 사이에 일대일 대응이 성립해야 한다. 이는 실수 전체의 모임을 자연수들과 대응하여 하나하나 순차적으로 세나갈 수 있다는 뜻이다. 그렇다면 임의의 실수의 부분집합을 선택해도 순차적으로 세나갈 수 있어야 한다. 우리는 실수의 특정 부분집합을 골라서 이럴 수 없음을 확인하고자 한다.
0과 1 사이에 있는 모든 실수의 모임을 생각하자.
0과 1 사이의 실수는 언제나 다음의 형식으로 기술된다:
ex) 0.1
0.22
0.12345678901
$0.a_1 a_2 a_3 a_4 \cdots$.
그리고 각 i 번째 소수점 $a_i$는 0 부터 9사이의 어떤 숫자이다.
0과 1 사이의 실수들을 순차적으로 세나갈 수 있어야 하므로 순서를 매겨서 다음과 같이 적자 : $x_1, x_2, x_3, x_4, \cdots$.
이를 다시 적으면,

여기서 0과 1의 사이의 모든 실수는 순차적으로 셀 수 있으므로
$x_i=0.a^i_1 a^i_2 a^i_3 \cdots$
꼴로 표현되어야 한다.
이 시점에서 다음과 같은 수를 생각해보자.
$x_i=0.a^i_1 a^i_2 a^i_3 \cdots$
여기서 각 i 마다 $a^i_i$ 가 만약에 3이라면 $b_i$는 4로
$a^i_i$ 가 3이 아니라면 $b_i=3$ 으로 준다.
그러면 X의 각 자리수 --는 --와 다르므로 X는 그 어떤 --와도 달라야한다. 이는 0과 1사이의 모든 실수는 -- 꼴이라고 한 것에 위배되어 모순이 발생한다.
이 모순은 자연수와 실수의 일대일 대응이 성립한다는 가정에서 비롯된 것이므로 원하는 결론이 도출된다.
참고
위의 논증을 칸토어 (Cantor, 1845-1918, 집합론 창시자)의 대각화 방법 (diagonal method)라 부릅니다.
생각해볼점
자연수 집합은 정수 집합에 속한다. 자연수가 아닌 정수들이 존재한다.
정수집합도 유리수 집합에 속한다. 역시 정수가 아닌 유리수들이 있다.
그런데도, 세 집합 사이에는 일대일 대응이 가능하다.
어째서 (직관과 대치되는) 상황이 발생하는가? 이는 적어도 자연수 집합, 정수집합, 유리수 집합이 전부 무한집합이기에 가능한 일이다.
그러나 모든 무한집합간에 일대일 대응이 가능한 것이 아니다.
무한 집합들 사이에도 (다소 놀랍게도!) 엄연히 차이가 있다.
자연수 집합과 실수집합의 경우처럼.
적어도 실수의 집합은 일일히 셀 수 없을만큼 자연수의 집합보다는 '크다'.
(집합론에서는 무한집합을 포함하여 집합의 크기를 기수, Cardinal Number, 라 부릅니다)
그렇다면 다음의 질문을 생각해 볼 수 있을 것이다.
질문: 자연수의 집합보다는 '크고' 실수의 집합보다는 '작은' 무한집합이 존재하지 않는가?
이 질문은 칸토어에 의해 처음 제기되었고, 다비트 힐베르트에 의해 1900년 세계 수학자 대회에서 제기된 23가지 중요한 문제들 중에서 1번 문제에 해당한다. 이를 연속체 가설이라 부른다.
이 문제는 '반증 불가능'리 1940년 쿠르트 괴델에 의해 증명되었고, 1963년 폴 코헨에 의해 '증명 불가능'이 증명되었다.
(이에 대한 자세한 논의는 집합률의 ZFC 공리계에 대한 이해를 필요로 합니다.)
결론적으로 답이 없다는 것이다. 참이라고 해도 상관없고, 거짓이라고 해도 무관하다.
결국 무엇을 참으로 받아들일지는 각자의 '선책'의 영역에 해당하며,
내 선택과 타인의 선택이 일치할 필요가 없다. 그것도 심지어 수학의 범주 하에서조차.
그렇다면, 다음의 질문도 생각해 볼 수 있다.
질문 우리가 중고등학교 시절에 숱하게 접해온 수학 안에서도 혹시 실상은 참도 거짓도 아닌데 반드시 그러해야 하는 것 처럼 받아들인
명제들이 있었을까요?
- (피타고라스의 정리) 직각 삼각형의 빗변의 길이의 제곱은 직각을 이루는 두 변의 길이의 제곱합과 같다.
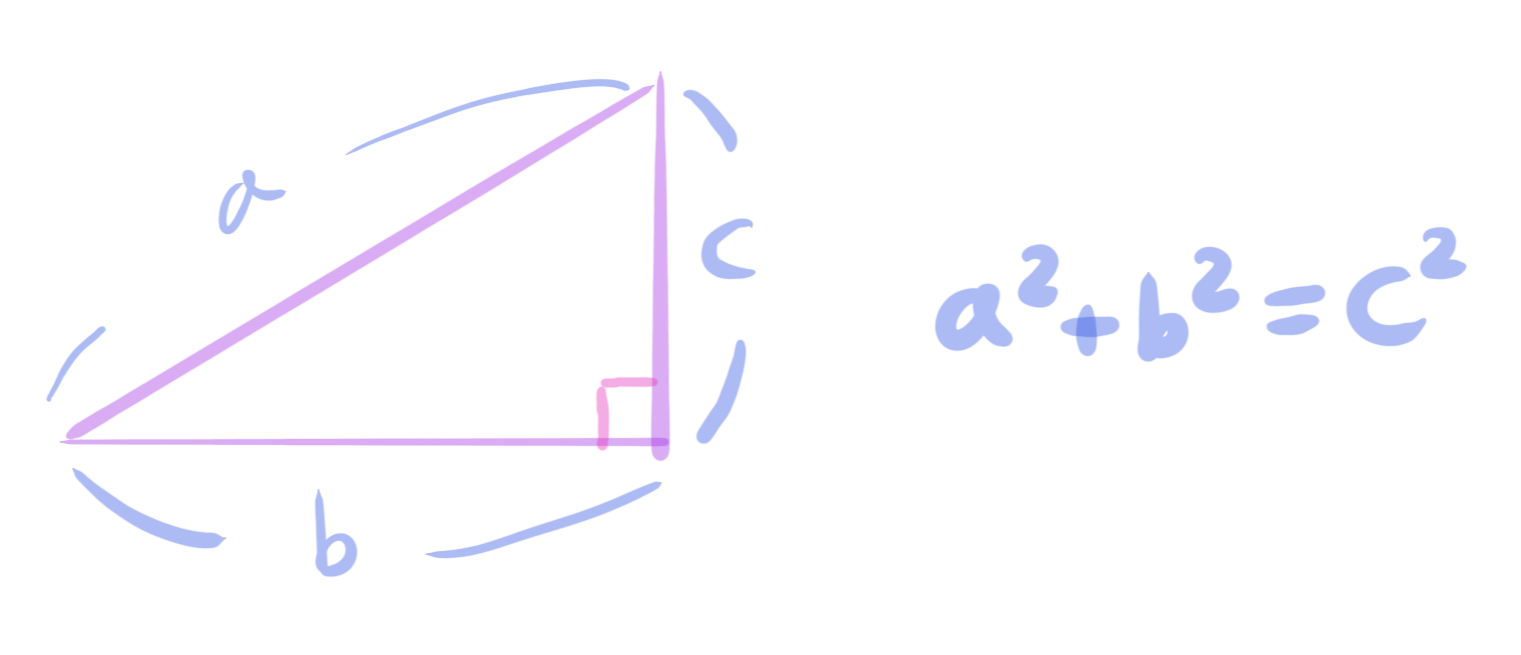
- (삼각형 공준) 모든 삼각형의 내각합은 180도 이다.

- 직사각형이 존재한다
- (등거리 공준) 평행한 두 직선의 거리는 어디에서나 일정하다
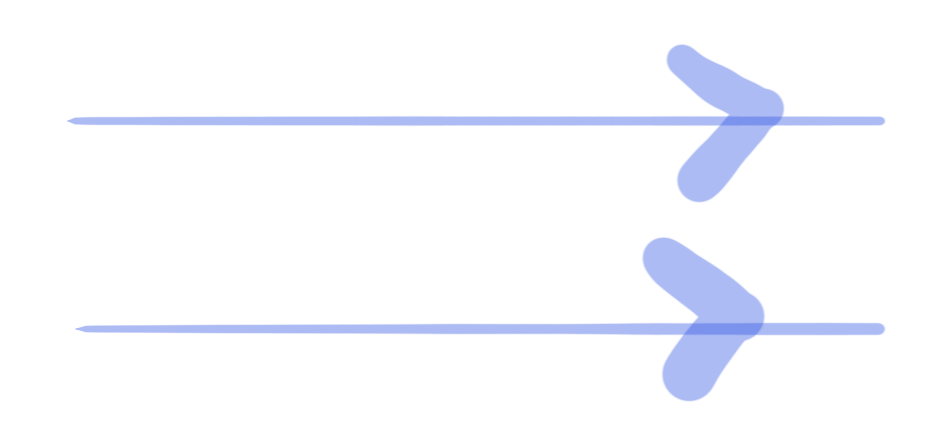
- (평행성 공준) 두 직선이 한 직선과 만나 이루는 두 동측내각의 합이 두 직각보다 작다면 이 두 직선을 무한히 연장할 때 그 두 동측내각과 같은 쪽에서 만난다.

사실은, 위의 다섯가지 문장은 수학적으로 전부 동치이다.
기원전 3세기에 쓰여진 유클리드 기하학 (우리가 중학교 시절에 배웠던) 원론은 다섯가지 약속 (공리)를 토대로 만들어졌고
그 중에서 다섯번째 공리가 평행선 공존에 해당한다.
그리고 19세기에 와서 제 5 공리를 부정해도 다른 공리와는 아무런 모순이 없음이 밝혀졌다. 마치 연속체 가설 처럼.
(제 5 공리를 부정하는 기하학을 비유클리드 기하학 non-Euclidian geometry, 현대 수학에서는 대개 리만기하학 Riemanninan geometry라 부른다. 이름에 해당하는 베른하르트 리만은 가우스의 제자이다.)
(비유클리드 기하학은 수수수학적으로만 주류에 해당하는 수학이 아니며, 현대통계학의 주류응 이루고 있는 베이지안 통계학, 코딩과 정보이론, 우리가 살아가는 물리적 시공간 등등에서 수학적 모델로서 자연스럽게 등장한다.)
(한편으로, 기원전 3세기에 형성된 '선입견'이 19세기에 이르러서 비로소 깨지기 시작했음을 생각해보면 현재 이 순간에도 불필요한 건입견을 정답으로서 생각하고 있진 않을지 돌아보게 되는 것 같습니다.)
오늘 수학교실의 결론
수학적 참과 거짓을 논하려면 공리의 선택을 필요로 한다.
특히나 무한집합들 처럼 직관과 실체가 대치될 수 있는 수학적 대상을 다루기 위해서는 적절한 공리의 선택은 필수불가결 하다.
그러나 적절한 공리의 체택은 각자 (그리도 인간의) 합리성에 의존하는 선택과 믿음의 영역이다. 나쁘게 표현하면 내가 주어진 대상을 어떻게 바라볼지 '색안경'을 정해야 그로부터 참과 거짓을 논할 수 있는 것이다.
다음 시간을 위한 질문들
- 자연수 집합의 수학적 정의가 뭔가요?
(혹자는 1,2,3,... 이라고 말씀하시겠지만, '...' 이라고 말하면 안 되는 것 아닌가요?)
- 왜 1+1=2 인가요?)
(왜 당연한걸 물어, 라고 불만을 제기하고자 하신다면 납득 가능하게 설명하실 수 있나요?)
- 왜 (-1)X(-1)= 인가요?
'직장인과 문과생을 위한 수학교실 (직문수)' 카테고리의 다른 글
| 6강. 역행렬과 행렬식의 의미, 선형대수학 Part B (0) | 2023.08.03 |
|---|---|
| 5강. 벡터공간과 행렬, 선형대수학 Part 1 (0) | 2023.08.02 |
| 4강. 군의 관점에서 살펴보는 지수법칙과 역함수 (0) | 2023.08.02 |
| 3강. 함수의 정의와 군 (0) | 2023.08.01 |
| 2강. 근의 공식과 대수학, 자연수 집합의 페아노공리계와 군의 정의 (0) | 2023.07.31 |



