다음 포스팅은 https://youtu.be/TAU6lRYS4y4 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
Quiz last time. $\left(e^{2 y}-y\right) \cos x \frac{d y}{d x}=e^{y} \sin 2 x$
SOl) This ODE is separable.
$$
\begin{aligned}
& \left(e^{2 y}-y\right) \frac{1}{e^{y}} d y=\frac{\sin 2 x}{\cos x} d x \\
& \sin 2 x=2 \sin x \cos x \\
& \left(e^{y}-y e^{-y}\right) d y=2 \sin x d x \\
& \int \quad \int e^{y}-y e^{-y} d y=2 \int \sin x d x \\
& =-2 \cos x+C \\
& \text { LHS }=\int e^{y} d y-\int y e^{-y} d y=e^{y}-\int {y e^{-y}dy}
\end{aligned}
$$
Integration by parts (I.B.P)
$$
\begin{aligned}
& u=u(x), =v(x) \\
& \int_{a}^{b} u(x) v^{\prime}(x) d x=\left.u(x) v(x)\right|_{a} ^{b}-\int_{a}^{b} u^{\prime}(x) v(x) d x \\
& \therefore \int u(x) v^{\prime}(x)+u^{\prime}(x) v(x) d x=u(x) v(x) \\
& \int y e^{-y} d y=-y e^{-y}+\int e^{-y} d y \\
& =-y e^{-y}-e^{-y}
\end{aligned}
$$
Here, $u=u(y)=y, v^{\prime}=v^{\prime}(y)=e^{-y}$
$$ u^{\prime}(y)=1, v=-e^{-y}
$$
In all,
$$
e^{y}+y e^{-y}+e^{-y(x)}=-2 \cos x+c \text {. }
$$
Hence, $y=y(x)$ is a function satisfying (*)
Applications of Separable ODEs
Example. Mixing Salt
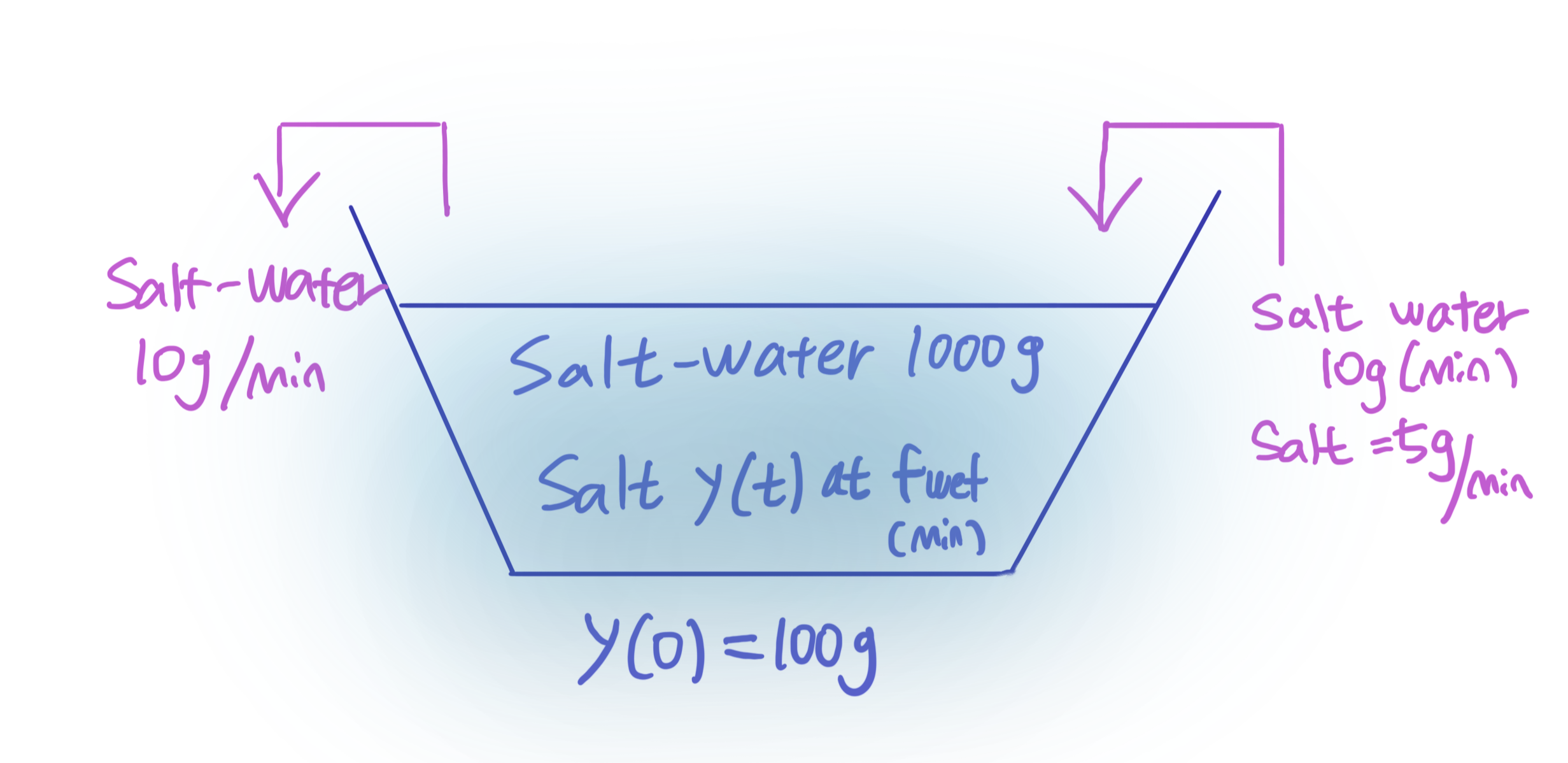
$y=y(t)$ the amount of salt at time $t$
Mathematical Modeling;
$$
\frac{d y}{d t}=y_{\text {input }}-y_{\text {output }}=5-\frac{y(t)}{1000} \times 10
$$
$$
\begin{aligned}
& y(0)=100 \\
& \text { Sol) } \frac{d y}{d t}=5-\frac{y(t)}{1000} \times 10 \\
& \Leftrightarrow \frac{d y}{500-y}=\frac{d t}{100} \\
& \iint \frac{d y}{500-y}=\int \frac{d t}{100}=\frac{t}{100}+C \\
& -\int \frac{d y}{y-500}
\end{aligned}
$$
$$
\begin{aligned}
& -\ln |y-500|=\frac{t}{100}+C \\
& \Leftrightarrow \ln |y-500|=-\frac{t}{100}+C \\
& \Leftrightarrow|y-500|=e^{-\frac{t}{100}+c}=c e^{-\frac{t}{100}}, c>0 \\
& \Leftrightarrow y-500= \pm c e^{-\frac{t}{100}} \\
& =c e^{-\frac{t}{100}}, c \neq 0 \\
& \Leftrightarrow y=y(t)=500+c e^{-\frac{t}{100}} \\
& 100=y(0)=500+C, C=-400
\end{aligned}
$$
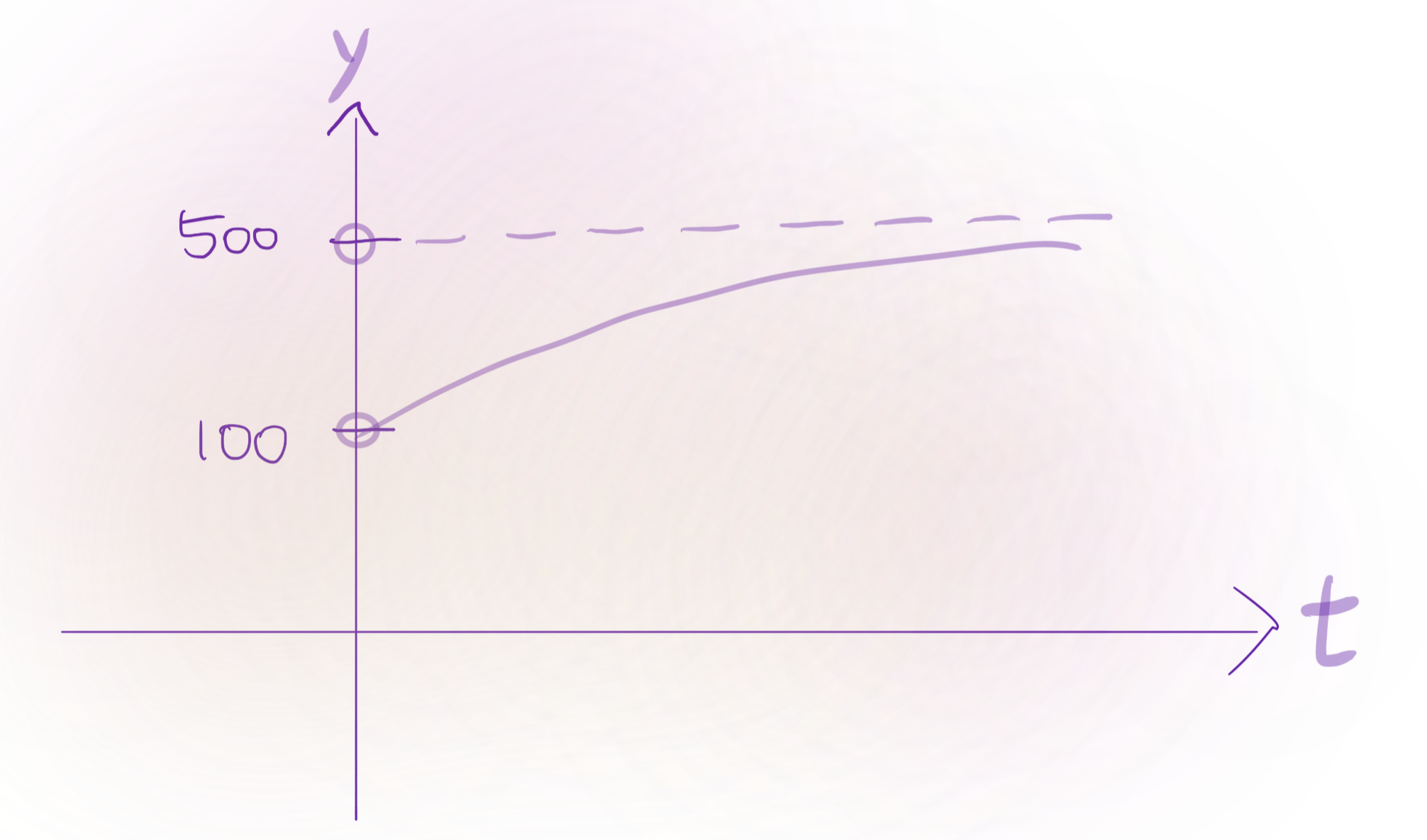
Hence
$$
y=y(t)=500-400 e^{-\frac{t}{100}}
$$
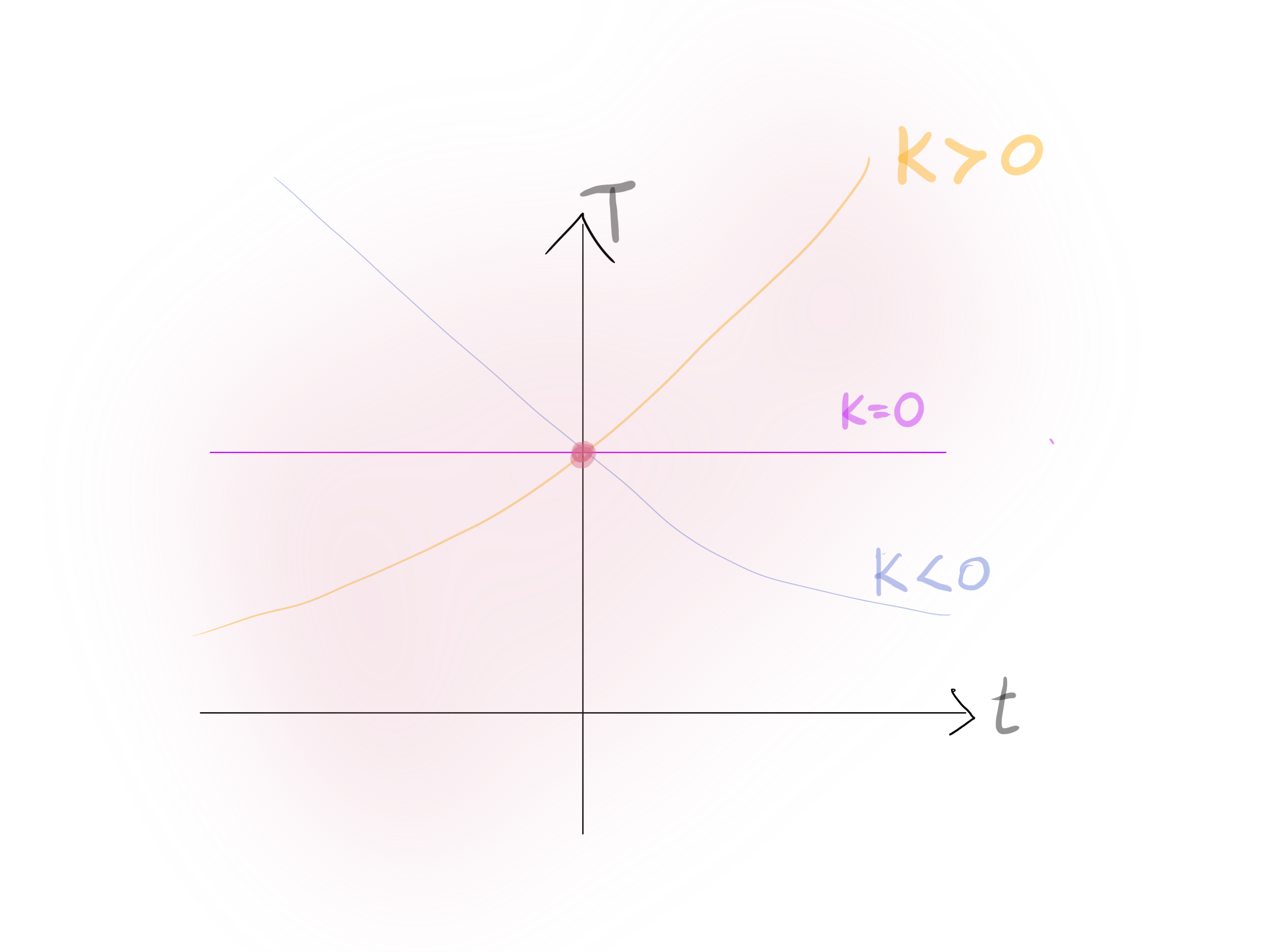
Example. Law of heating.

Question. $T=T(t)$ ?
By Newton's law,
$$
\frac{d T}{d t}=K(T(t)- T_{outside})
$$
: Separable ODE.
$$
\begin{aligned}
& \Leftrightarrow \frac{d T}{T-45}=k d t \\
& \Rightarrow \int \frac{d T}{T-45}=\int k d t \\
& =k t+C \\
& \ln |T-45|=k t+C
\end{aligned}
$$
$$
\begin{aligned}
& \Leftrightarrow|T-45|=e^{k t+c}=c e^{k t}, c>0 \\
& \Leftrightarrow T-45= \pm c e^{k t}=c e^{k t}, c \neq 0 \\
& \Leftrightarrow T=T(t)=45+c e^{k t} \\
& 70=T(0)=45+C, C=25 \\
& T(t)=45+25 e^{k t}.
\end{aligned}
$$
Caution. The difficulty of solving separable ODES depends on the difficulty of simplifying integrations in step 2.
Question. What if the 1St-order ODE is NOT separable?
$$
y^{\prime}=\frac{d y}{d x}=\frac{x^{3}+3 x y^{2}}{3 x^{2} y+y^{3}}: \text { NOT separable. }
$$
Quiz. Solve the following ODEs:
1) $y^{\prime}=\frac{d y}{d x}=\frac{x-2 y+2}{2 x-4 y+4}$,
2) $y^{\prime}=\frac{d y}{d x}=\left(\frac{y}{x}\right)^{2}-\frac{y}{x}+1$.
'다 까먹었지만 수학은 하고싶어, 미분방정식' 카테고리의 다른 글
| 미분방정식 4강. 완전 미분방정식 (0) | 2023.07.28 |
|---|---|
| 미분방정식 3강. 전미분과 Chain rule, 완전 미분방정식 (0) | 2023.07.28 |
| 미분방정식 1강. 변수분리형 미분방정식 (0) | 2023.07.26 |
| 수학을 다 까먹은 내가 미분에 대해 알아갈만한 이유 (0) | 2023.06.30 |
| 가장 간단한 미분방정식 풀어보기 (0) | 2023.06.29 |


