다음 포스팅은 https://youtu.be/J0c_f5sx8LU 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
Question. $y^{\prime}=\frac{x^{3}+3 x y^{2}}{3 x^{2} y+y^{3}}$ : not separable.
How to solve non-separable ODEs?
Intuitive-example.
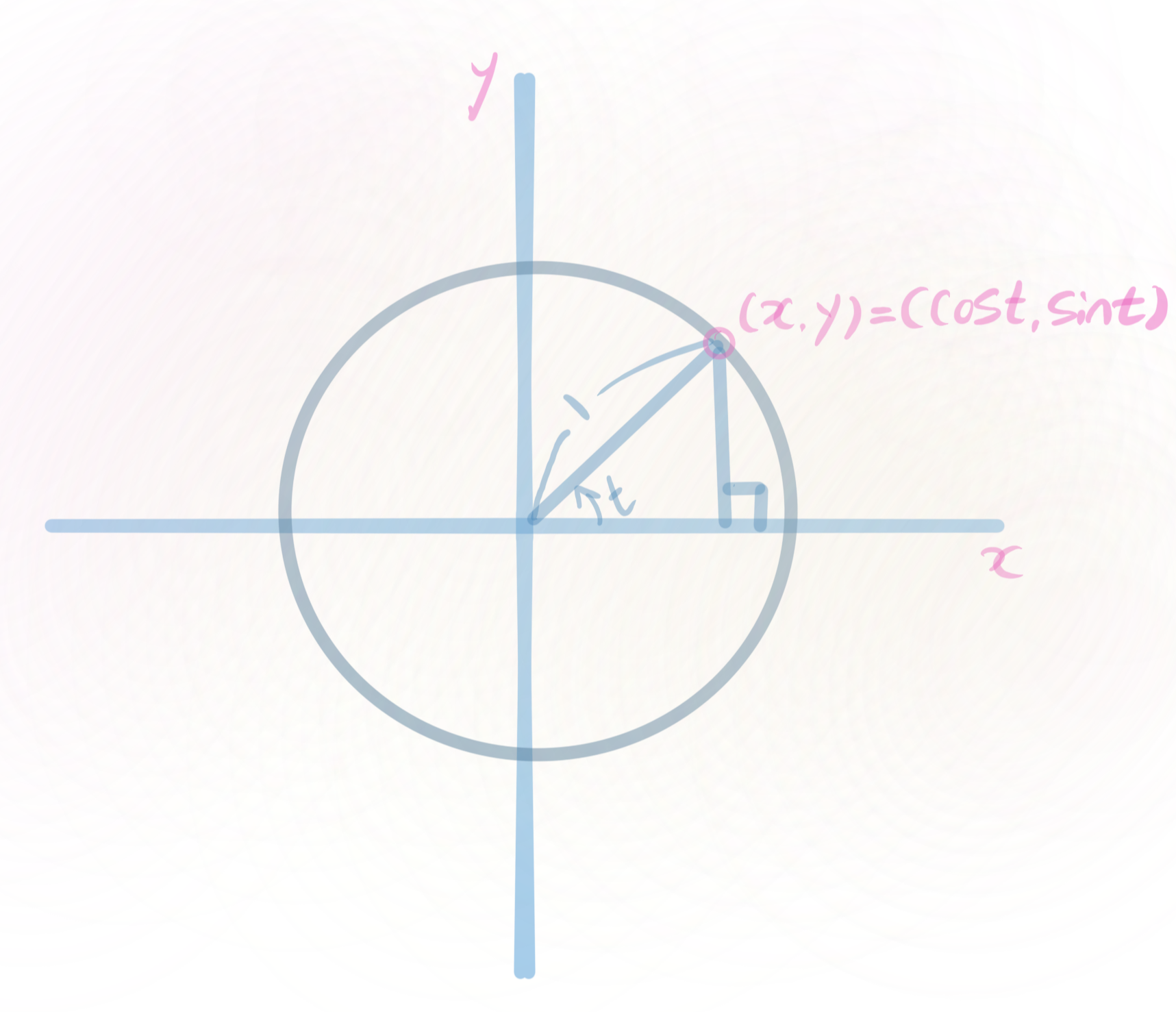
Here,
$$
\begin{aligned}
& x=x(t)=\cos t \\
& y=y(t)=\sin t
\end{aligned}
$$
Assume $u=u(x, y)=u(x(t), y(t))=u(t)$.
$$
\Rightarrow \frac{d u}{d t}=u^{\prime}(t)=?
$$
Chain-rule (미적분학에서 라이프니츠 법칙, 부분적분법과 함께 가장 중요한 기술 중 하나).
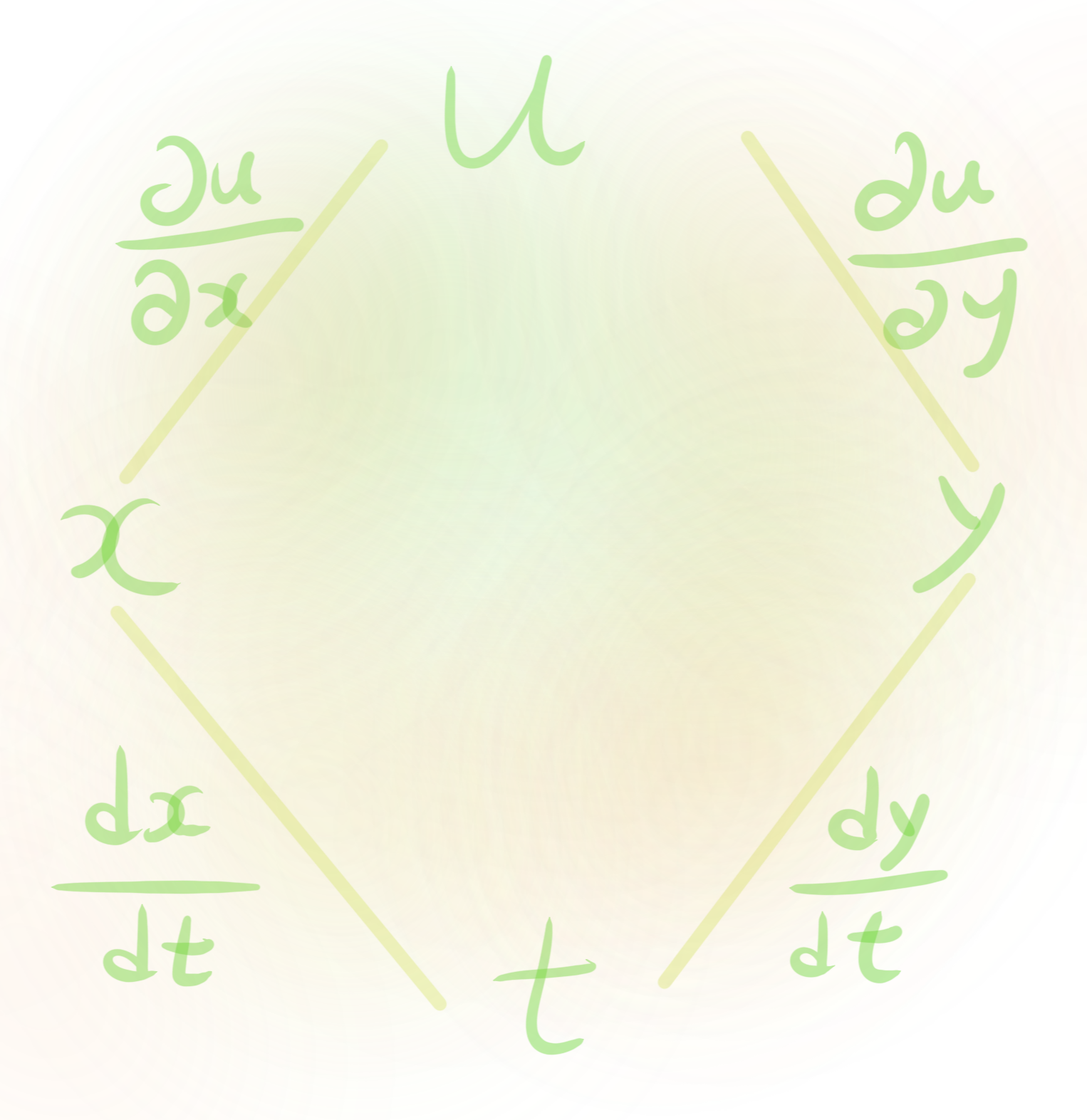
partial derivative " $\partial$ ".
usual derivative " $d$ ".
$$
\frac{d u}{d t}=\frac{\partial u}{\partial x} \cdot \frac{d x}{d t}+\frac{\partial u}{\partial y} \cdot \frac{d y}{d t}
$$
$\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}$ partial derivatives with respect to $x, y$ respectively.
example. $u=u(x, y)=x+2 y$.
$$
\frac{\partial u}{\partial x}=1, \quad \frac{\partial u}{\partial y}=2 \text {. }
$$
Example. $u=u(x,y)=x^{2}+2 y^{3}$.
$$
\frac{\partial u}{\partial x}=2 x, \frac{\partial u}{\partial y}=6 y^{2} .
$$
Example. $u=x^{2} y+4 x y^{2}$.
$$
\begin{aligned}
& \frac{\partial U}{\partial x}=2 x y+4 y^{2}, \\
& \frac{\partial U}{\partial y}=x^{2}+8 x y .
\end{aligned}
$$
$$
u=u(x, y)=u(x(t), y(t))=u(t) .
$$
By the chain-rule,
$$
\frac{d u}{d t}=\frac{\partial u}{\partial x} \cdot \frac{d x}{d t}+\frac{\partial u}{\partial y} \frac{d y}{d t} .
$$
Multiply dt in each Side:
$$
d u=\frac{\partial U}{\partial x} d x+\frac{\partial u}{\partial y} d y
$$
: called the total differential 전미분 (or differential form 미분형식) of u.
Back to the question.
$$
y^{\prime}=\frac{d y}{d x}=\frac{x^{3}+3 x y^{2}}{3 x^{2} y+y^{3}} \text { : not separable }
$$
$$
\begin{aligned}
& \Leftrightarrow d y=\frac{x^{3}+3 x y^{2}}{3 x^{2} y+y^{3}} d x, \\
& \times\left(3 x^{2} y+y^{3}\right)\left(3 x^{2} y+y^{3}\right) d y=\left(x^{3}+3 x y^{2}\right) d x . \\
& \Leftrightarrow\left(x^{3}+3 x y^{2}\right) d x-\left(3 x^{2} y+y^{3}\right) d y=0 .
\end{aligned}
$$
Expect: $d u=\frac{\partial u}{\partial x} d x+\frac{\partial u}{\partial y} d y$
$$
\Leftrightarrow\left\{\begin{array}{l}
\frac{\partial u}{\partial x}=x^{3}+3 x y^{2}, \\
\frac{\partial u}{\partial y}=-\left(3 x^{2} y+y^{3}\right) \\
d u=0
\end{array}\right.
$$
such a differential equation is called an exact Differential equation.
'다 까먹었지만 수학은 하고싶어, 미분방정식' 카테고리의 다른 글
| 미분방정식 5강. 완전 미분방정식으로 일반적인 1차 미분방정식 풀기 (0) | 2023.07.29 |
|---|---|
| 미분방정식 4강. 완전 미분방정식 (0) | 2023.07.28 |
| 미분방정식 2강. 변수분리형 미방과 미적분학, 수학적 모델링 (0) | 2023.07.26 |
| 미분방정식 1강. 변수분리형 미분방정식 (0) | 2023.07.26 |
| 수학을 다 까먹은 내가 미분에 대해 알아갈만한 이유 (0) | 2023.06.30 |



