다음 포스팅은 https://youtu.be/BJg7apGVIME의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
Separable equation
Definition. Given $\frac{d y}{d x}=f(x, y), y=y(x)$, we say it is separable if
$$
f(x, y)=\left\{\begin{array}{l}
g(x) h(y), \text { or } \\
\frac{g(x)}{h(y)}, \text { or } \\
\frac{h(y)}{g(x)}, \text { or } \\
\frac{1}{g(x) h(y)}
\end{array}\right.
$$
Example. $y^{\prime}=\frac{y}{1+x}$
$$
\begin{aligned}
& \Leftrightarrow \frac{d y}{d x}=\frac{y}{1+x}, \\
& \Leftrightarrow d y=\frac{y}{1+x} d x, \\
& \Leftrightarrow(1+x) \\
& \Leftrightarrow(1+x) d y=y d x .
\end{aligned}
$$
$$
\Leftrightarrow y d x-(1+x) d y=0
$$
The recipe to solve a separable ODE
Assume $\frac{d y}{d x}=f(x, y)=\frac{g(x)}{h(y)}$
Step 1. Separate two variables in each side
i.e., $h(y) d y=g(x) d x$
Step 2. Take integrations in each side
$$
\int h(y) d y=\int g(x) d x
$$
and proceed necessary calculations
Step 3. Simplify as $y=y(x)$
Example. $y d x-(1+x) d y=0$
Sol) This ODE is separable
$$
\begin{aligned}
& y d x=(1+x) d y \\
\Leftrightarrow & \frac{d x}{1+x}=\frac{d y}{y} \\
\Rightarrow & \int \frac{d x}{1+x}=\int \frac{d y}{y} \\
\Leftrightarrow & \ln |1+x|+C=\ln |y|, C \text { any constant } \\
& \ln A=B, A=e^{B} \\
\Leftrightarrow & |y|=e^{\ln ||+x \mid+C} \\
= & e^{\ln |+x|} \cdot e^{c}
\end{aligned}
$$

$\Leftrightarrow|y|=\widetilde{C}|1+x|, \widetilde{C}$ any positive Constant
$\Leftrightarrow y= \pm \widetilde{C}(1+x)$
$\Leftrightarrow y=c(1+x), \quad C$ any non-zero constant
$\therefore$ this is called a general solution
Remark. Let $C=0$. Then it is easy to see $y=0$ also becomes a solution.
: called the Singular Solution
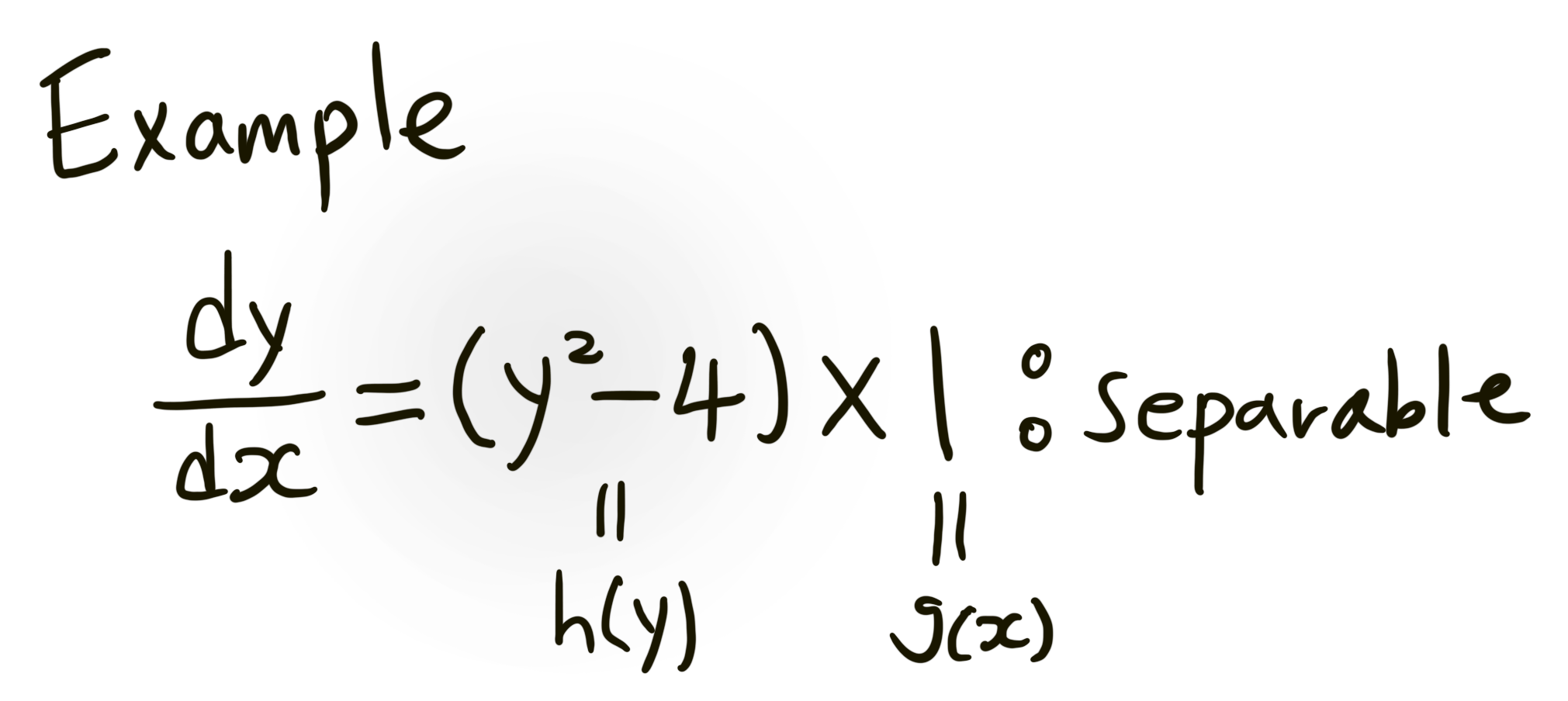
$$
\begin{aligned}
& \text { So1) } \frac{d y}{y^{2}-4}=d x \\
& \Rightarrow \int \frac{d y}{y^{2}-4}=\int 1 d x=x+C
\end{aligned}
$$
Fractional decomposition; $\frac{1}{y^{2}-4}=\frac{1}{(y-2)(y+2)}$
$$
\begin{aligned}
& =\frac{A}{y-2}+\frac{B}{y+2} \\
& x(y-2)(y+2) ; \quad 1=A(y+2)+B(y-2) \\
& y=-2: 1=-4 B, \quad B=-\frac{1}{4} \\
& y=2: \quad 1=4 A, A=\frac{1}{4}
\end{aligned}
$$
$$
\begin{aligned}
& \text { LHS }=\int \frac{1}{y^{2}-4} d y \\
& =\int \frac{1}{4} \frac{1}{y-2}-\frac{1}{4} \frac{1}{y+2} d y \\
& =\frac{1}{4} \int \frac{1}{y-2} d y-\frac{1}{4} \int \frac{1}{y+2} d y \\
& =\frac{1}{4} \ln |y-2|-\frac{1}{4} \ln |y+2| \\
& =\frac{1}{4} \ln \frac{|y-2|}{|y+2|}=\frac{1}{4} \ln \left|\frac{y-2}{y+2}\right| \\
& =x+C, C \text { any Constant. } \\
& x 4: \ln \left|\frac{y-2}{y+2}\right|=4 x+C \\
& \Leftrightarrow\left|\frac{y-2}{y+2}\right|=e^{4 x+C}=e^{4 x} \cdot e^{C} \\
& =\widetilde{c} \cdot e^{4 x}, \tilde{c}>0
\end{aligned}
$$
$$
\begin{aligned}
& \Leftrightarrow \frac{y-2}{y+2}= \pm \widetilde{c} e^{4 x} \\
& =c e^{4 x}, \quad c \neq 0
\end{aligned}
$$
: a general solution Note $\frac{1}{A \cdot B}=\frac{1}{B-A}\left(\frac{1}{A}-\frac{1}{B}\right)$
$$
=\frac{1}{B-A} \frac{B-A}{A B}
$$
$$
\begin{aligned}
& \frac{1}{y^{2}-4}=\frac{1}{(y-2)(y+2)} \\
& A=y-2, B=y+2 \\
& =\frac{1}{(y+2)-(y-2)}\left(\frac{1}{y-2}-\frac{1}{y+2}\right) \\
& =\frac{1}{4}\left(\frac{1}{y-2}-\frac{1}{y+2}\right)
\end{aligned}
$$
Quiz. Solve the following ODE:
$$
\left(e^{2 y}-y\right) \cos x d y=e^{y} \sin 2 x d x
$$
'다 까먹었지만 수학은 하고싶어, 미분방정식' 카테고리의 다른 글
| 미분방정식 3강. 전미분과 Chain rule, 완전 미분방정식 (0) | 2023.07.28 |
|---|---|
| 미분방정식 2강. 변수분리형 미방과 미적분학, 수학적 모델링 (0) | 2023.07.26 |
| 수학을 다 까먹은 내가 미분에 대해 알아갈만한 이유 (0) | 2023.06.30 |
| 가장 간단한 미분방정식 풀어보기 (0) | 2023.06.29 |
| 이 수업에서 하고자 하는 것 (0) | 2023.06.29 |

