다음 포스팅은 https://youtu.be/UIlC9ikSpNc 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
Symmetric group.
Definition. $n \in \mathbb{N}$. $S_{n}:=\left\{f:\left(\begin{array}{c}1 \\ \vdots \\ n\end{array}\right) \longrightarrow\left(\begin{array}{c}1 \\ \vdots \\ n\end{array}\right) \mid f\right.$ is 1-1, onto $\}$.
Then $\left(S_{n}, 0\right)$ is a group, called the symmetric group.
We call the element - of $S_{n}$ a permutation
Remark. $\left|S_{n}\right|=n !$
ex) $n=3, S_{3}\left(\leadsto\left|S_{3}\right|=3 \times 2\times 1 \mid=6\right)$

Proposition. Every permutation in $S_{n}$ can be written by disjoint cycles.
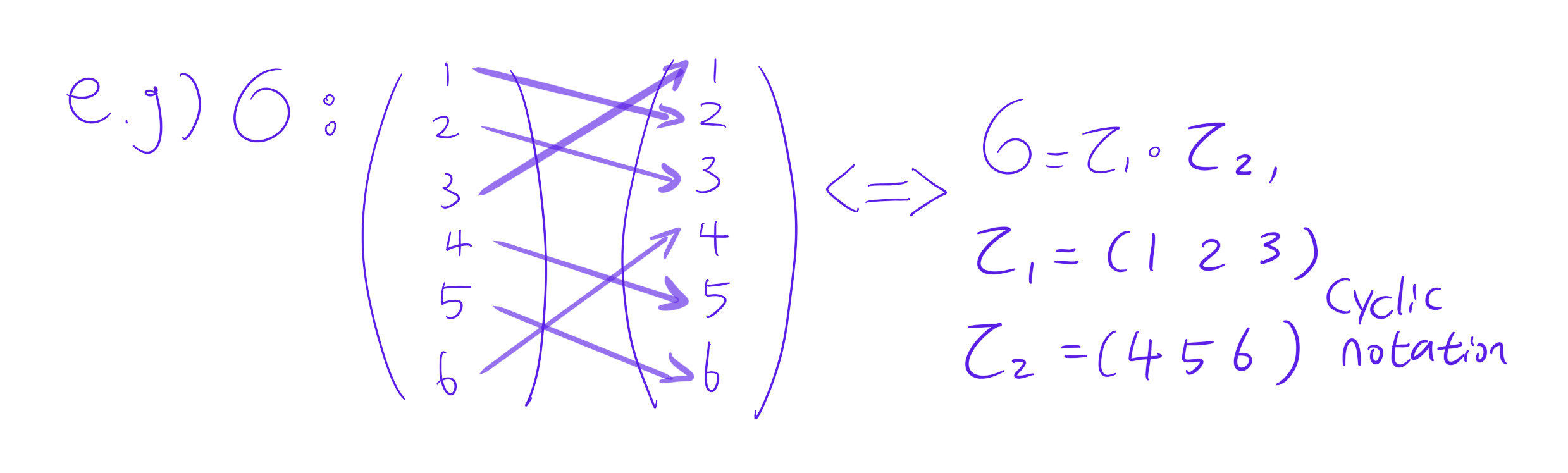
$\begin{aligned}
& 1 \rightarrow 2 \rightarrow 3 \rightarrow 1 \text {, } \\
& 4 \rightarrow 5 \rightarrow 6 \rightarrow 4 \text { or, } \sigma=\tau_{2} \circ \tau_{1} \text {. }
\end{aligned}$
In this way, we can $\sigma={\tau_{1} \circ \tau_{2} \circ \cdots \circ \tau_{r}}(r \geq 1)$
Remark.
$(1,2 \cdots n)=(1 n) \cdot(1 n-1) \ldots \circ(12)$
In general, $\left(i_{1} i_{2} \ldots i_{n}\right)=\left(i_{1} i_{n}\right)\left(i_{1} i_{v-1}\right) \ldots . .\left(i_{1} i_{2}\right)$
e.g)
$
\begin{aligned}
(1\quad 2\quad 3\quad 4)= & (1 \quad 4) \cdot(1\quad 3) \cdot(1\quad 2) \\
& 1 \rightarrow 2 \longrightarrow 2 \longrightarrow 2 \\
& 2 \longrightarrow 1 \longrightarrow 3 \longrightarrow 3 \\
& 3 \longrightarrow 3 \longrightarrow 1 \rightarrow 4 \\
& 4 \longrightarrow 4 \longrightarrow 4 \longrightarrow 1
\end{aligned}
$
Definition. $(i j)$ is called the transposition : 1-cycle, 2-element.
Remark. Every permutation Can be written by Compositions of disjoint cycles, and every cycle is compositions of transpositions.
$\operatorname{Rmk}(1\quad 3)=(1\quad 3)(2\quad 4)(4\quad 2)$
$=(1\quad 3)(2\quad 4)(4\quad 2)(1\quad 2)(2\quad 1)$
Proposition. (Conservation of parity) Let $\sigma \in S n$.
Write $\sigma=\tau_{1}\circ \cdots \circ \tau_{k}$
$=\tau_{1}^{\prime} \circ \ldots \circ \tau_{k}^{\prime}$
$\tau_{i} \tau_{j}^{\prime}$ transpositions.
$\Rightarrow k+k^{\prime}$ is even.
Lemma. Let $\tau_{1} \cdots . . \tau_{k}=i d, \tau_{i}$ transposition.
Then $k $ is even.
Proof of proposition. Let $\sigma=\tau_{1} \circ \cdots \circ \tau_{k}=\tau_{1}^{\prime} \circ \cdots \circ \tau_{k}^{\prime}$
$\begin{aligned}
\Rightarrow & \left(\tau_{1} \circ \cdots \circ\tau_{k}\right)^{-1}\left(z_{1}^{\prime}\circ \cdots \circ \tau_{k}^{\prime}\right)=i d \\
& \left(z_{k}^{-1} \circ \cdots \circ \tau_{1}^{-1}\right)\left(\tau_{1}^{\prime} \circ \cdots \circ \tau_{k}^{\prime}\right)=i d
\end{aligned}$
$\stackrel{\text { Lemma }}{\Rightarrow} k+k'=$ even.
Proof of lemma.
Take any integer $m \in s 1, \cdots, n\}$.
Let $j_{m}$ be the largest number of $\tau_{k}$ which has $m$.
$
\text { e.g) } \begin{aligned}
\sigma & =(1\quad 2)(3\quad 4)(2\quad 3)(5\quad 2) . \\
m & =1 .
\end{aligned}
$
Then there are 4 possible cases: for distinct $x, y, m, n$.
(1) $(m\quad x) \cdot(m\quad x)=i d$
(2) $(m\quad y) \circ(m\quad x)=(m\quad x)(y\quad x)$
(3) $(n \quad x) \cdot(m\quad x)=(m\quad n)(x\quad n)$
(4) $(n \quad y) \cdot(m \quad x)=(m \quad x)(n \quad y)$
Thus, $m$ Can be contained only in $j_m^{-1}$ the transposition.
Definition. Given $\left(S_{n}\right)$ a Symmetric group,
then $\sigma \in S n$ is even if $\sigma$ is written by even numbers of transpositions.
Definition. Define $sgn : S_n \rightarrow \left\{1,-1\right\}$, by $sgn(\sigma)=1$ if $\sigma$ is even and $sgn(\sigma)=-1$ if $\sigma$ is odd.
Then $sgn$ is well-defined
$
\left(\because \sigma_{1}=\sigma_{2} \Rightarrow \operatorname{sgn}\left(\sigma_{1}\right)=\operatorname{sgn}\left(\sigma_{2}\right)\right)
$
Moreover, sgn is a group homomorphism.
$
\text { i.e., } v \sigma_{1}, \sigma_{2} \in S_{n_{1}} \quad g_{n}\left(\sigma_{1}\cdot \sigma_{2}\right)=\operatorname{Sgn}\left(\sigma_{1}\right) \times sgn\left(\sigma_{2}\right)
$
Definition. $\left.\operatorname{ker}(\operatorname{sgn})=\{\sigma \in S_{n} \mid \operatorname{sgn}(\sigma)=1\right\} \unlhd S_{n}$.
We call $\operatorname{Ker}(sgn)=: A_n$ the $n$th alternating subgroup.
of $S_n$. (From the def, Au is a normal subgp of sn)
$
\begin{aligned}
& \text { Definition (Determinant) } A \in Mat_{n \times n}(\mathbb F), \\
& \operatorname{det} A=\sum_{\sigma \in S_{n}} \operatorname{sgn}(\sigma) \prod_{i=1}^{n} \sigma_{i \sigma(i)}
\end{aligned}
$
'기초부터 대학원 수학까지, 추상대수학' 카테고리의 다른 글
| 28. 추상대수학 (h) 직접곱, 직접합 (0) | 2023.09.07 |
|---|---|
| 26. 추상대수학 (g) 제1,2,3 동형정리 (0) | 2023.08.31 |
| 25. 추상대수학 (f) 정규부분군간의 1-1 대응 (0) | 2023.08.30 |
| 24. 추상대수학 (e) 정규부분군의 정의 (0) | 2023.08.23 |
| 23. 추상대수학 (d) 군작용과 케일리 정리 (0) | 2023.08.18 |