다음 포스팅은 https://youtu.be/v6Dy51r1xJU 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
강의 16. 리만의 복소함수론과 대수기하학의 아름다움
지금까지 함께 알아온 것들
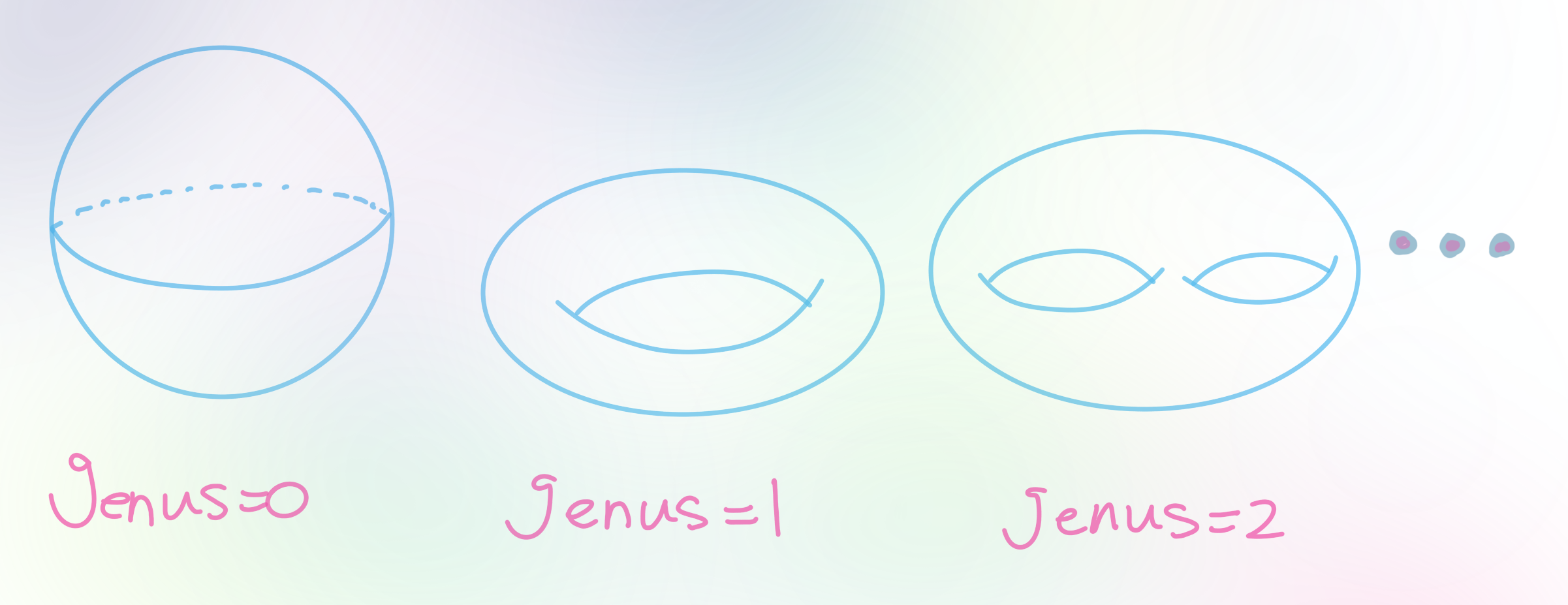
- (14강) 미분기하학은 가우스 곡률이 0이 아닌 내적이 주어진 구부러진 곡면 및 고차원 공간들 (다양체 manifold)들을 공부하는 수학이다. 2차원 곡면의 경우에 모든 점에서 가우스 곡률이 상수 (constant)인 (단순연결된) 곡면은 정확히 세 가지 경우가 있다

- (14강) 가우스-보네 정리, $\frac{1}{2\pi}\iint_{S} cdA=X(s)$= S의오일러의지표
는 곡면의 형상 (shape)을 내적 (Riemannian metric)으로 부터 아무리 변형해도 근본적인 차이가 있음을 가르쳐준다. 이를 요약해서, 공간을 "찰흙 덩어리"로서 바라보면 구($S^2$)와 원한면은 서로 다른 공간들에 해당하며, 이들의 차이는 오직 곡면에서 구멍의 갯수 (genus)로만 분류된다.
(11강) 미적분학의 기본정리에 따르면 미분가능한 함수 $y=f(x)$에 대해 $\int_{a}^{b} f^{\prime}(x) d x =f(b)-f(a), a<b $ 가 성립한다.
이 정리는 미분계수 $y=f'(x)$의 적분을 함수 $y=f(x)$를 구할 수만 있다면 쉽게 계산할 수 있음을 알려준다. 그러나 일반적으로 이 전제는 문제가 된다.
이 경우, 함수 $y=h(x)$에 대해 $\int_{a}^{b} h(x) d x$를 구하는데 있어서 테일러 급수는 크게 요긴하다.
정의 (테일러 급수) 무한번 미분가능한 함수 $h: \mathbb{R} \longrightarrow \mathbb{R}$에 대하여 각점 $p∈\mathbb R$에서 $$h(x)\sum_{k=0}^{\infty} \frac{h^{(n)}(p)}{n !} (x-p^{n})$$으로 표현될때, 우리는 이러한 함수 $h$를 해석적 함수 (analytic function)이라고 부른다. 여기서 $n!=x×(n-1)×...×2×1, h^({n})(p)$는 $h(p)$의 $(p)$에서 $n$번 미분한 값 (the nth derivative of $h$ at $p$)이다.
예시)
$$
\begin{aligned}
& e^{x}=\sum_{n=0}^{\infty} \frac{1}{n !} x^{n} \\
& \sin x=\sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2 n+1) !} x^{2 n+1}, \cos x=\sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2 n) !} x^{2 n} .
\end{aligned}
$$
해석적 함수 $h(x)=\sum_{n=0}^{\infty} \frac{h^{(n)}(P)}{n !}(x-P)^{n}$ 에 대해서는
$$
\int_{a}^{b} h(x) d x=\int_{a}^{b} \sum_{n=0}^{\infty} \frac{h^{(n)}(p)}{n !}(x-p)^{n} d x=$$ $$d(x)=\sum_{n=0}^{\infty} \frac{h^{(n)}(P)}{(n+1){!}}((b-p)^{n}-(a-p)^{n+1})$$으로 미분하여 $h(x)$가 되는 함수를 몰라도 여전히 적분을 구할 수 있다.
(2강) 이차방정식 $ax^2+bx+c=0$의 해는 $x=\frac{-b±\sqrt{b^2-4ac}}{2a}$에 해당한다. 여기서 제곱근 (root$sqrt$) 내부는 음수가 될 수도 있으므로 일반적으로 이차방정식의 해는 실수가 아니라 허수 $i(i^2=-1)$를 포함하는 복소수 $C=\{a+bi:a,b\in\mathbb R\}$의 원소에 해당한다.
코멘트 미적분을 말해오다가 방정식의 근의 공식에 대해 이야기 하는게 이상하지 않으신가요? 무슨 연결고리를 기대할 수 있을까요?
(1,2강) 결국 우리가 정말 아는 것이라곤 숫자의 덧셈과 곱셈 뿐입니다.
특히나 변수 $x$ 및 숫자의 덧셈과 곱셈으로 만든 함수
$y=a_{n} x^{n}+a_{n-1} x^{n-1}+...+a_{1} x+a_{0} \text {, } a_{i}$는 숫자를 다항함수 (the polynomial function)라고 한다.
이 강의의 목적 지금까지 해온 곡면의 미분기하학과 위상수학 이야기 전부가 실상 다항함수 및 다항식을 살펴보는 것에 불과함에 대해 살펴보고자 한다. (복소해석학, 복소기하학, 대수기하학, 정수론에 해당.) 결론도 매우 비자명하지만 이를 서술하는 리만의 복소함수론 (가우스 아래에서 박사학위 논문)은 어떠한 의미에서든지 실로 수학적 아름다움의 극치이다.
그런데, 이 이야기들은 필연적으로 실수 (real number) 대신에 복소수를 토대로 서술해야 합니다. 그러므로 왜 굳이 이러한 수체계를 고려하는게 타당한지 살펴볼 필요가 생깁니다.
복소수를 고려해야 하는 몇가지 당위성
1. 대수학의 기본정리 Fundamental theorem of algebra
임의의 $n$차 다항식 $a_{n} x^{n}+a_{n-1} x^{n-1}+...+a_{1} x+a_{0}$의 해는 총 ($n$)개 존재하며 이 또한 모든 해는 (실수도 복소수로 간주) 복소수에 해당한다.
예시) $n=2$, 이차방정식의 근의 공식
2. 연산의 이유
우리 마음의 고향 $\mathbb R^2=\{({a,b)}:a,b\in\mathbb R\}$는 벡터공간이다. 즉, 벡터간의 덧셈과 벡터와 스칼라간의 스칼라곱만 허용된다. 그러나, 두 벡터 간의 '곱셈'은 말하지 못한다. 그런데 벡터 $(a,b)$를 복소수 $a+bi$로 표기하면 다음과 같이 자연스럽게 곱셈이 정의된다:
$(a,b)\longleftrightarrow a+bi, (c,d)\longleftrightarrow c+di$,
$(a+bi)\times(c+di)=ac+adi+bci+bdi^2$=$(ac-bd)+(ad+bc)i$
복소수간의 덧셈의 정의는 $\mathbb R^2$ 에서 벡터간의 덧셈과 같다.
$(a+bi)+(c+di)=(a+c)+(b+d)i$
$(a,b)+(c,d)=(a+c,b+d)$
3. 물리학적 자연스러움
물리학에서 에너지는 어떤 양의 제곱근으로 표현되므로, 에너지 보존법칙이 성립하려면 제곱해서 음수가 되는 허수를 포함하는 수체계를 사용하는게 자연스럽다. 일례로 고전역학에서 에너지 (해밀토니안)을 양자화해서 얻어지는 파동함수의(슈뢰딩거) 방정식은 허수를 사용해서 표현된다.
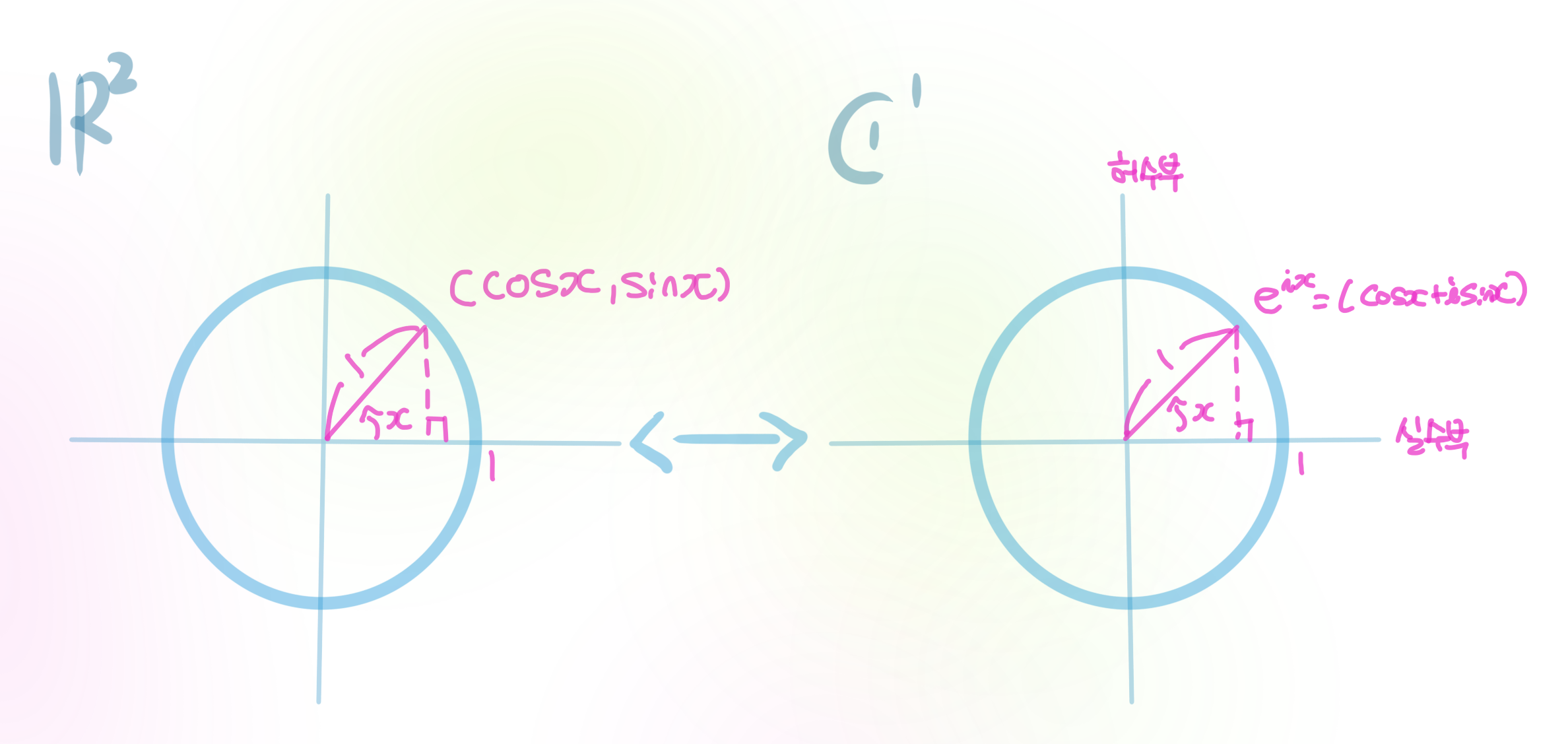
4. 오일러공식 $e^{ix}=cosx+isinx$ 유도는 $e^i,cosx,sinx$의 테일러 급수에 $x$대신에 $ix$를 대입하면 된다.
이 공식은 평면의 회전을 복소 자수함수 $e^{ix}$로 표현할 수 있음을 알려준다.
한걸음을 비약하는 관찰과 자연스러운 질문
우리는 벡터공간 $\mathbb R^2$를 복소평면 $\mathbb C'$으로서 바꾸어서 살펴보고자 하고있습니다. 그런데 지금까지 배워온 스토리에 따르면 $\mathbb R^2$는 2차원 곡면 중에서도 가장 단순한 평면에 해당합니다. 그렇다면 임의의 2차원 곡면들을 비록 지금까지는 실수를 토대로 살펴보았지만 마찬가지로 적절히 복소수 위에서 살펴볼 수 있는 것 아닐까요?
이 답은 수학적으로 yes입니다. 임의의 '실수위의 2차원 곡면'은 사실 '복소수 위의 1차원 곡선'에 해당합니다. 특히 후자로서 보는 곡면을 리만곡면 (Riemann surface)이라고 부릅니다.
그런데 말입니다. 특정 구조를 갖는 집합을 공부하기 위해서는 그러한 집합들간의 구조를 잘 호환해주는 함수들도 마땅히 지정해주어야 합니다. 현대 우리가 고려하는 집합은 복소수를 사용하고자 하므로 함수 또한 그러해야 할 것입니다. $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$대신에 $f: \mathbb{C}^{1} \longrightarrow \mathbb{C}^{1}$.
또한 우리는 결국 미적분학을 잘 활용할 수 있는 함수들을 사용하기를 원합니다. 아는게 그거 밖에 없으니까요.
즉, 우리는 '복소 해석적' 함수를 사용하고 싶은 것입니다.
$(x,y)\in\mathbb R^2\longleftrightarrow$ $x+iy\in C'$의 관계에 대하여
앞으로 복소수는 $x+iy='z'$로 표기한다.
그리고, 만약에 $\alpha-i\beta$도 반드시 해가 된다. 그러므로 복소수 $z=x+iy$는 대개 $x-iy=\mathbb Z$와 함께 생각하는게 자연스럽고 $\mathbb Z$를 $z$의 켤레복소수라고 부른다.
즉 $(x,y)$는 $(z,\overline{z})$와 일대일 대응이 되고, 켤레복소수 $\overline{z}는 $z$로부터 허수부의 부호를 바꿈으로서 얻어진다.
$(x,y)\longleftrightarrow(z\mathbb Z)$로부터 다음도 성립한다.
미분가능한 함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}$에 대하여
$\frac{\partial f}{\partial z}=\frac{1}{2}({\frac{\partial f}{\partial x}})-i\frac{\partial f}{\partial y}$
$\frac{\partial f}{\partial \mathbb Z}=\frac{1}{2}({\frac{\partial f}{\partial x}})-i\frac{\partial f}{\partial y}$
우변은 우리가 지금까지 다루어온 $x,y$의 편미분이고 좌면은 $z,\mathbb Z$에 대한 편미분이다.
앞으로 $\mathbb{R}^{2}$는 전부 $\mathbb {C'}$으로 간주한다.
정의1 (복소해석적 함수 complex analytic function)
$\mathbb C'$의 (열린) 부분집합 $S⊆C'$위에서 정의된 함수 $f: S \longrightarrow \mathbb{C}^{1}$가 다음의 조건을 만족하면
$f$를 복소해석적 함수라고 부른다: $S$의 각 점 $P\in S$마다 $$f(z)\sum_{n=0}^{\infty} \frac{f^{(n)}(p)}{n !} z^n$$으로 표현 가능하다.
관찰 복소해석적 함수의 테일러급수 표현에서 $z$의 켤레복소수 $\mathbb Z$의가 등장하지 않는다. 즉 복소해석적 함수는 $\mathbb Z$에 대해 편미분 하면 $\frac{\partial f}{\partial\mathbb Z}=0$이어야 한다.
다소 비자명하나, 이 사실은 복소해석젓 함수가 되는 여하와 동치이다.
정의2 (복소해석적 함수=홀로몰픽 함수 holomorphic function)
$\mathbb C'$의 열린 부분집합 $S⊆\mathbb C'$위에서 정의된 함수 $f: \mathbb{S} \longrightarrow \mathbb{C}^1$가 $S$의 모든 점 $P\in S$에서 $\frac{\partial f}{\partial \mathbb Z}(p)=\frac {1}{2}\frac{\partial f}{\partial x}(p)+i\frac{\partial f}{\partial y}(p)$=0 이면 $f$를 홀로몰픽 혹은 복소해석적 함수라고 부른다.
관찰 복소해석적 함수 $f: S \longrightarrow \mathbb C$가 주어져 있다고 가정하자.
각 $P\in S$마다 함수값 $f(p)$는 복소수이므로 실수부와 허수부로 나누어서
$f(p)=u(p)_iu(p)$로 표현할 수 있다. 즉,
$f=u+iu, u, U:S\longrightarrow\mathbb R$이다.
그런데 $f$는 복소해석적이므로 각 $P\in {S}$마다
$\frac{\partial f}{\partial \mathbb Z}(p)=\frac {1}{2}(\frac{\partial f}{\partial x}(p)+i\frac{\partial f}{\partial y}(p))$
=$\frac {1}{2}(\frac{\partial}{\partial x}(u+iu)(p)+i\frac{\partial}{\partial {y}}(u+iu)(p))$
=$\frac {1}{2}(\frac{\partial u}{\partial x}\frac{\partial u}{\partial y}(p))+i(\frac{\partial u}{\partial {y}}+\frac{\partial u}{\partial x}(p))$
이다. 즉, 다음을 얻는다:
$f=u+iu:S\longrightarrow\mathbb C$, $u, U:S\longrightarrow R$가 복소해석적 함수인 여하는 다음의 두 식을 만족하는 것과 동치이다:
$\frac{\partial u}{\partial x}=\frac{\partial u}{\partial y}$
on $S$ : 이 식들을 합쳐서 코사리만 방정식이라고 부릅니다.
$\frac{\partial u}{\partial y}=-\frac{\partial u}{\partial x}$
정의3 $f=u+iu:S\longrightarrow\mathbb{C}$가 각 $P\in S$에서
코사-리만 방정식을 만족하면 $f$를 복소해석적 함수라 부른다.
코멘트 결국 복소해석적 함수는 테일러 급수로 표현가능한 복소함수를 말하고, 테일러급수는 미적분학을 잘 사용하기 위한 방법에 해당한다. 이를 토대로 지금부터 몇가지 마법을 소개한다.
복소함수론의 아름다움 (다음 시간에 시계열분석 Time Series Analysis에서 사용)
코시적분정리 (Augustin-Louis-Cauchy, 1814년 제안, 1825년 증명)
복소해석적 함수 $f:S\longrightarrow\mathbb C$가 주어져 있다고 가정하자. 여기서 $S$는 단순연결 (S의 내부의 임의의 폐곡선이 한 점으로 수축가능한 공간)이라고 가정한다.
그러면 언제나 다음이 성립한다:$S$내부의 임의의 폐곡선 $C$에 대해 $f$를 선적분 (line integral)하면 항상 0이다.
즉, $\int_{c} fdz=0$이다.
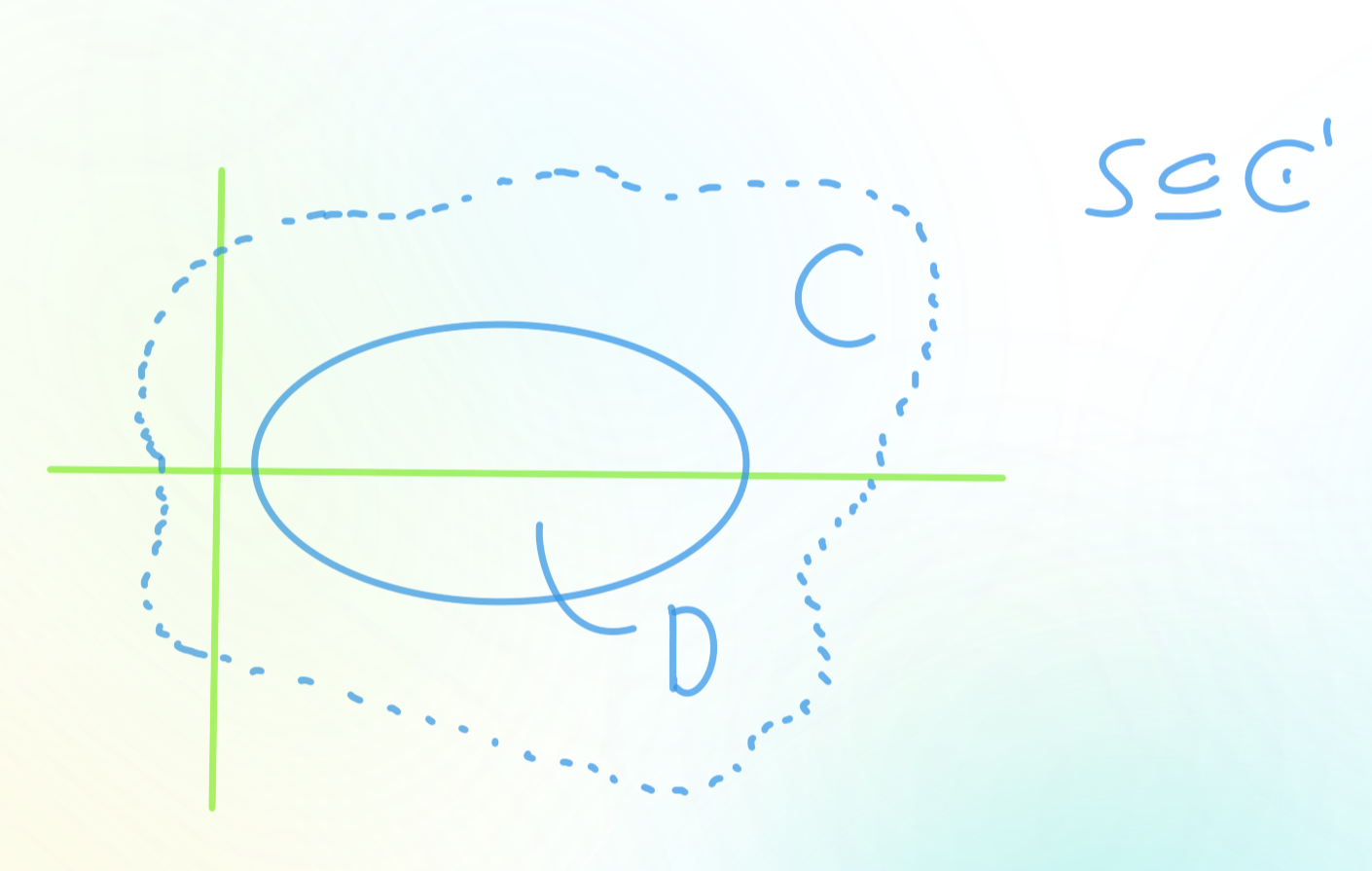
복습 (그린정리) $\int_{c}(u,U)\cdot dr$=$\iint_{d}(\frac{\partial u}{\partial x}-\frac{\partial u}{\partial y})dxdy$
증명 $f=u+iu,u, U:S\longrightarrow\mathbb R$로 두자.
정의 3에 의해 $\frac{\partial u}{\partial y}-\frac{\partial u}{\partial y}$,$\frac{\partial u}{\partial y}=-\frac{\partial u}{\partial x}$이다.
그러면 $\int_c fdz=\int_c(u+iu)(dx+idy)$
=$\int_c[(udx-udy)+i(udx+udy)]$
=$-\iint_{D} (\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y})dxdy+i\iint_D(\frac{\partial u}{\partial x}-\frac{\partial u}{\partial y})dxdy$
=0이다. Q.E.D.
폐곡선 C 내부에 점 P가 주어질 때, 계산을 해보면
$\frac{1}{2 \pi i} \int_{C}\frac{1}{z-p}dz=1$를 얻는다. 이것을 일반화하면 다음을 얻는다:
코시 유수정리(Residue Theorem, 1826년 제안, 1831년 증명)
함수 $f:S(⊆C)$ 안쪽에 점 P에서 $f(z)=$$\sum_{n=-\infty}^{\infty}a_n(z-p)^n$$ 으로 '표현'하자. 그러면 다음이 성립한다:
$\frac{1}{2 \pi i} \int_{C}fdz=a_{-1}$
코멘트 사실은 마법이 발생한것이다. 적분 계산을 안하고도, 즉, $f$를 급수로 표현한 시점에서 우린 이미 적분값을 아는 것이다.
코시적분공식 (1831년 증명)
복소해석적 함수 $f:S(⊆)C$\longrightarrow {C}$ 가 주어지고 $S$ 내부의 폐곡선 $C$를 임의로 선택하자. 그러면 폐곡선 $C$
내부의 임의의 점 $P$에 대해 다음이 성립한다:
$f(p)=\frac{1}{2 \pi i} \int_{C} \frac{f(z)}{z-p} d z$
증명 $f$는 복소해석적 함수이므로 $f(z)=\sum_{n=0}^{\infty} \frac{f^{(n)}(P)}{n !}(z-P)^{n}$$으로 표현하자. 그러면 $$\frac{f(Z)}{z-p}=\sum_{n=-1}^{\infty} \frac{f^{(n+1)}(P)}{(n+1)}(z-P)^{n}$$ 이다. 따라서 유수정리는 ${\frac{f(z)}{z-p}}$에 적용하면 $a_1$=f(p)$이므로 $\frac{1}{2 \pi i}$ $\int_{C}\frac{f(z)}{z-p}fdz=a_{-1}=f(p)$이므로 증명이 끝난다. Q.E.D.
리만사상정리(Riemann Mapping Theorem, 1851)
복소평면 $C$와 같지 않은 단순연결된 (열린) 부분집합 $S$는 언제나 상반평변 (Upper half plane)간에 일대일 대응인 복소해석적 함수가 존재한다.
코멘트 상반평면은 가우스곡률이 음의 상수인 단순 연결된 유일한 곡면이다. 그러므로 만약에 복소해석적 함수가 내적까지 보존해준다면 복소평면 $C$와 같지 않은 단순연결된 (열린)부분집합 $S$는 상반평면으로 정말 간주해도 된다는 의미가 된다.
슈왈츠 보조정리 (Schwarz Lemma, 1890) 상반평면 간의 임의의 일대일 대응인 복소해석적 함수는 가우스 곡률이 음의 상수인 내적을 언제나 보존한다.
코멘트 이 노트의 작성자는 1차원 복소공간 및 일반적인 차원의 복소공간들에 대해서 임의의 일대일 대응 복소해석적 함수가 보존해주는 내적들에 대해 연구해서 박사학위를 받았습니다.
복소해석적 함수에 대한 리만의 관점:'함수가 정의되는 곡면을 찾는다'
우리가 잘 아는 함수들은 대부분 일변수 함수 $f: \mathbb{R} \longrightarrow \mathbb{R}$에 해당한다.
예시) $\begin{aligned}& \text { (4) } f(x)=x, f(x)=\sin x, f(x)=\cos x, f(x)=e^{x} \\
& f(x)=\sqrt{x}=x^{\frac{1}{2}}, f(x)=\sqrt{x^{3}-x}=\left(x^{3}-x\right)^{\frac{1}{2}}, \infty\end{aligned}$
이 함수들의 정의역 (그리고 그에 따라서 공역)을 복소수 $z$로 대채하여 함수들을 복소해석적 함수 ($Z$변수가 없으므로)로 만들어 보고자 한다, $f:C\longrightarrow C$
예시) $f(z)=\sin z, f(z)=\cos z, f(z)=e^{z}$,
$f(z)=\sqrt{z}=z^{\frac{1}{2}},
f(z)=\sqrt{z^{3}-z}=\left(z^{3}-z\right)^{\frac{1}{2}}, \cdots$
그런데, 여기서 문제가 하나 발생하는데, 위의 두 함수는 함수로서 잘 정의되지 않는 점이다.
설명 0이 아닌 복소수 $z$는 $z=|z|\cdot\frac{z}{|z|}=re^{i\theta}$로 표현 할 수 있다.
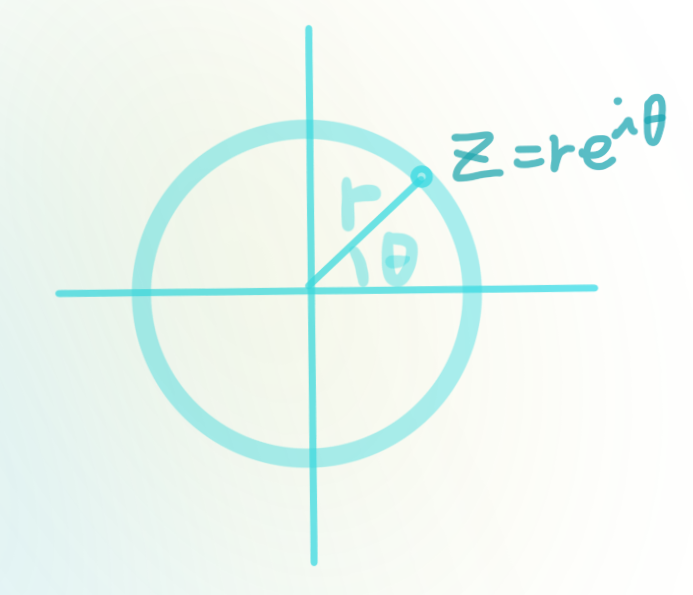
$\theta$는 $x$축에서 반시계 방향으로 회전한 값이므로 매바퀴 회전할때마나 바뀌지 않는다. 즉,
$e^{i\theta}=e^{i(\theta+2\pi)}=e^i{(\theta+4\pi)}=...=e^{i(\theta+2n\pi)},n$은 임의의 정수.
이제 함수 $f(z)=\sqrt z=z^{\frac{1}{2}}$을 살펴보자.
$f(z)=z^{\frac{1}{2}}=(re^{i\theta})^\frac{1}{2}=r^\frac{1}{2}e^{i\frac{\theta}{2}}$이어야 한다.
한바퀴 회전을 통해 $\theta$대신에 $\theta+2\pi$를 우변에 대입하면
$f(z)=(re^{i(\theta+2\pi)})^{\frac{1}{2}}$=$r^\frac{1}{2}e^{i\frac{\theta}{2}}\cdot e^{i\pi}$
$=-r^{\frac{1}{2}}e^{i\frac{\theta}{2}}$
$=-f(z)$-f(z)이다.
즉 한바퀴 회전하면 함수값은 $f(z)$와 $-f(z)$ 총 2개를 갖는다. 이는 함수의 정의에 의해 각 $z$마다 함수값은 반드시 하나 존재해야함과 상충된다.
결론적으로 $\theta$를 0부터 $2\pi$ 까지 회전시킬 수 있다면 $f(z)=z^{\frac{1}{2}}$는 잘 정의되지 않는다.
그러므로, 우리는 정의역을 복소평면 $C'$전체가 아니라 한바퀴 회전이 불가능하게 끔 0부터 양의 $x$축을 찢어버리고자 한다.
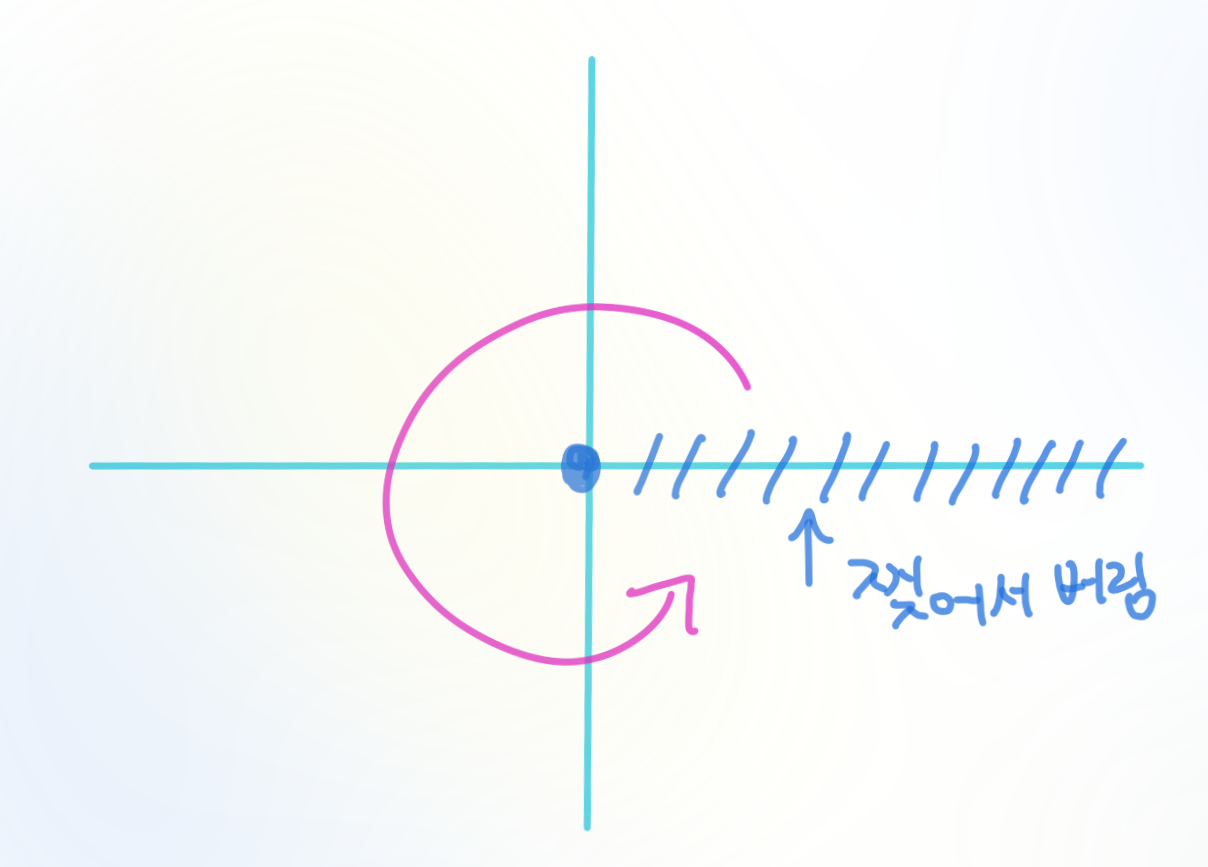
즉, $f: C-[0,∞)\longrightarrow C$로서 $f(z)=\sqrt z=z^{\frac{1}{2}}$을 생각하면 위와 같은 문제가 발생하지 않으므로 함수는 잘 정의된다.
다 적었는가? 그렇다. 함수의 정의역을 적절히 제한함으로서 적어도 $f(z)=\sqrt z$는 복소해석적 함수로서 잘 정의된다.
그러나 리만은 여기서 관찰 및 생각을 멈추지 않았다.
매바퀴를 기점 ($\theta=0,2\pi,4\pi,6\pi$,...)으로 함수값은 $f(z)$에서 $-f(z)$로 바뀌는게 문제이므로,
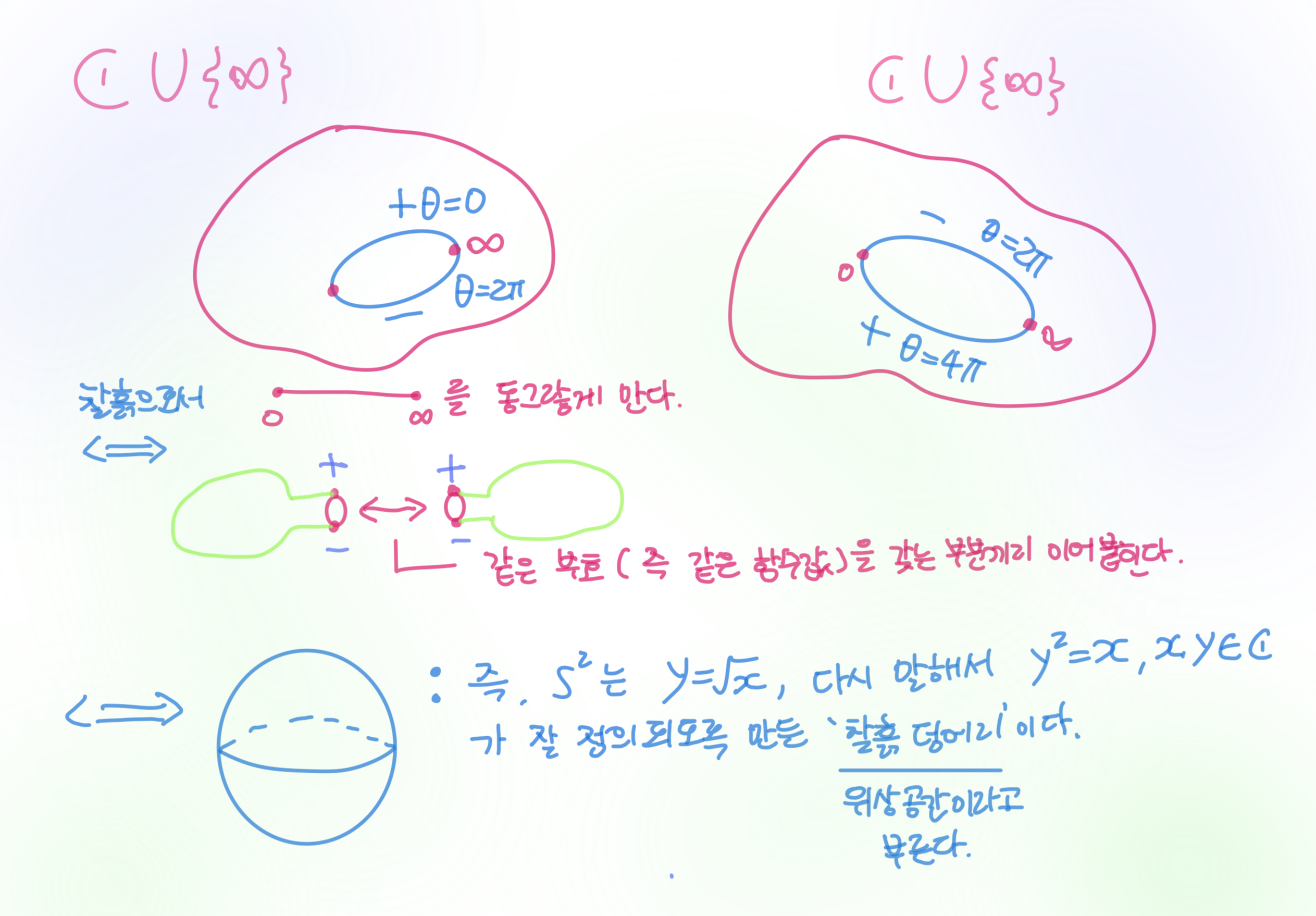
함수가 정의되는데 문제가 발생하는 부분을 이어붙여서 유일한 값을 갖는 함수로서 잘 정의되는 공간을 '찰흙 덩어리'로서 만들자
는 생각을 한다.

이 각각의 평면을 ∞를 포함하여 찰흙덩어리로서 '대충'그리자.
이 생각의 방식을 $f(z)=\sqrt {z^3-z}$에도 똑같이 적용하면 회전에 따라서 함수값이 +$f(z)$와 $-f(z)$두 값 모두 가능하다.
그러므로 $f(z)=\sqrt{z-3-z}$가 함수로서 잘 정의되도록 잘라내야 하는 구간: [-1,0],[1,∞])


리만곡면과 대수기하학 (Riemann Surface, Algebraic Geometry)
마법 비록 위의 관찰들은 $y=\sqrt x$ 및 $y=\sqrt{x^3-x}$에서 출발하여 그 함수들이 복소해석적 함수로서 잘 정의되는 곡면들이 sphere 및 torus 임을 확인했지만, 사실은 더 나아가서 다음이 성립한다:
(1) Sphere 는 찰흙 덩어리로서 $\left\{(x, y) \in \mathbb{C}^{2}: y^2=x\right\}$로 표현된다.
(2) Torus 는 찰흙 덩어리로서 $\left\{(x, y) \in \mathbb{C}^{2}: y^2=x^3-x\right\}$로 표현된다.
(3) 일반적으로 각 리만곡면마다 복소변수 2개 $(x,y)$인 어떤 다항식 $f(x,y)$이 존재해서 리만곡면은 찰흙덩어리로서 $\left\{(x, y) \in \mathbb{C}^{2}: f(x, y)=0\right\}$로 표현된다.
(4) 각 리만곡면이 구멍의 수 (genus) $g$는 리만곡면에 대응되는 복소변수 2개 $(x,y)$인 다항식의 최고차항의 차수 $(d)$와 대응된다: $g=\frac{(d-1)}{(d-2)}{2}$ ex)sphere:d=2, torus:d=3
매우 비자명한 결론 경계면이 없는 곡면의 기하학적 이해는 이 곡면에 대응되는 '다항식'을 이해하는 것에 불과하다!
이는 곡면의 이해를 위해 내적을 도입해서 가우스 곡률을 알고 가우스-보네 정리를 거쳐서 곡면의 오일러지표를 토대로 곡면을 구멍의 수 (genus)로 분류할 수 있음과 결론부는 일치할지라도 결론에 이르는 중간 과정은 다를 뿐더러 '내적'을 이해하고자 하는 미분기하학의 철학과는 사뭇 다른 것이다. 수학계에서 해석적 함수 및 다항함수의 해집합의 기하학적 구조를 공부하는 분야를
대수기하학 (algebraic geometry)이라고 부른다.

코멘트 대수기하학은 미분기하학으로는 다 둘 수없는 수학적 정보들을 구체적으로 다루도록 하는 렌즈겹 도구가 된다. 특히나 통계학습이론의 한 연구자는 통계학을 대수기하를 토대로 처음부터 새롭게 구성해야 한다는 강한 주장을 펼치기도 한다. 우리는 지금까지 보아온 미분기하 및 대수기하 통계학에 어떻게 녹아있는지 살펴보는 것으로 수학교실을 마무리 짓고자 한다.
마지막 시간 기하학의 렌즈로 바라보는 통계학의 아름다움
'직장인과 문과생을 위한 수학교실 (직문수)' 카테고리의 다른 글
| 17강. 통계학에 녹아있는 기하학의 아름다움 (0) | 2023.08.08 |
|---|---|
| 15강. 미분기하의 아름다움 (0) | 2023.08.06 |
| 12,13,14강. 다변수 미분법의 직관에 대한 설명 (0) | 2023.08.05 |
| 11. 미적분학의 기본정리와 적분의 아름다움 (0) | 2023.08.05 |
| 10. 다변수 미분법의 직관적 이해와 수학, 물리학의 현대적 태동 (0) | 2023.08.05 |



