다음 포스팅은 https://youtu.be/2ulgaG7BUgU 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
지난 시간 마지막
함수 $f:\mathbb{R}\longrightarrow \mathbb{R}$에 대해 임의이 0이 아닌 숫자 $h$에 대해서
$\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$이 존재한다면 우리는 이 값을 함수 $y=f(x)$의
미분계수 (derivative)라고 부르며 $f'(x)$로 표시한다.
질문 일변수 함수 $y=f(x)$의 미분법을 토대로
이변수 함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}$의 미분을 어떻게 정의하는지
$(x, y) \longmapsto f(x, y)$
자연스러울까요?
시도 벡터공간 $R^2$에 내적 <$\cdot,\cdot$>이 주어져 있다고 가정하자. (내적이 있어야 벡터의 크기를 말할 수 있다.)
함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}$를 고려하고
$(x, y) \longmapsto f(x, y)$
크기가 1인 벡터 $d=(p_1,d_2)∈\mathbb{R}^2$를 고정하자
만약에 벡터 $p=(p_1,p_2)∈\mathbb{R}^2$에 대해서
$\lim _{h \rightarrow 0} \frac{f(p+h d)-f(p)}{h}$가 존재한다면
이를 함수 $Z=f(x,y)$의$P$에서 $d$방향으로의
방향 미분계수 (directional derivative)라 부르고
$D_{d} f(p)=\lim _{h \rightarrow 0} \frac{f(p+h d)-f(p)}{h}$로 표시한다.
관찰 일변수함수의 미분법을 흉내내어서 이변수 함수 $Z=f(x,y)$의 방향 미분계수를 정의했습니다. 그런데 만약에 방향미분계수가 적절한 미분법의 정의가 되려면 일변수함수의 경우와 같이 적어도 연속함수가 되어야 타당합니다. 그러나 아쉽게도 일반적으로 그렇지 않습니다. 다음의 예시를 살펴봅시다:

$P=(0,0)$으로 선택하면 그 어떤 방향 $d=(d_1,d_2)$ 를 선택하여도 $D_{d} f(p)=\lim _{h \rightarrow 0} \frac{f(p+h d)-f(p)}{h}=0$이 된다.

그런데 $z=f(x,y)$는 함수값이 0에서 1로 급변할 수 있으므로 연속적으로 값이 변하지 않는다. 즉 $f$는 연속함수가 아니다. 다시 말해서 함수 $f$는 원점에서 모든 방햐에 대해서 비록 방향미분계수가 정의되지만 연속함수가 아니다. 이는 우리가 일변수함수의 미분계수로부터 얻어낸 성질과 대지되므로 미분법의 올바른 일반화라 할 수 없다.
코멘트 비록 방향미분계수 자체가 이변수함수의 미분법을 의미하지는 못하더라도 여전히 매우 요긴하게 사용됩니다.
내적에 해당하는 행렬 $\left(\begin{array}{cc}\langle(1,0),(1,0)\rangle & \langle(1,0),(0,1)\rangle \\\langle(0,1), (1,0)\rangle & \langle(0,1),(0,1)\rangle\end{array}\right)$을 항등행렬 $\left(\begin{array}{ll}
1 & 0 \\0 & 1\end{array}\right)$로 고른 가운데 (즉, 유클리드 기하 하에서)
방향 $d$을 틀별히 (1,0)과(0,1)로 선택하는 경우,
$\begin{aligned}
& D_{(10)} f(p)=\lim _{h \rightarrow 0} \frac{f(p+h(1,0))-f(p)}{h}=\frac{\partial f}{\partial x}(p) \text {, } \\
& D_{(0,1)} f(p)=\lim _{h \rightarrow 0} \frac{f(p+h(0,1))-f(p)}{h}=\frac{\partial f}{\partial y}(p)
\end{aligned}$
라고 적고, $\frac{\partial f}{\partial x}(p)$과$ \frac{\partial f}{\partial y}(p)$를 각각 $Z=f(x,y)$를 $x$방향과 $y$
방향으로 편미분계수 (partial derivative)라고 부른다.
7강 복습 벡터공간 $R^2$에 내적 <$\cdot,\cdot$>이 주어질 때,
두 벡터 $a,b∈R^2$간의 각도 $\theta$를 다음의 수식으로 정의했다: $\langle a, b\rangle=\|a\| \cdot\|b\| \cdot \cos \theta$
$\text { , }\|a\|=\sqrt{\langle a, a\rangle},\|b\|=\sqrt{\langle b, b\rangle} \text {. }$

이변수 함수의 미분의 정의 벡터공간 $R^2$에 내적 <\cdot,\cdot>이 주어졌다고 가정하자. 함수 $f:\mathbb{R}^2\longrightarrow \mathbb{R}$가 주어지되 모든 벡터 $p\in\mathbb{R}^2$에 대해서 다음의 조건을 만족하는 벡터 $\begin{aligned}\nabla f(p) \\\end{aligned}\in\mathbb{R}^2$가 존재한다면 우리는 $f$를 미분가능함수라 부르고 $\nabla f(p)$를 $p$에서의 gradient vector (구배 연산자)라 부른다:
각 $p\in\mathbb{R}^2마다 $\nabla{f}(p)$가 존재하여
$\begin{aligned}
& \lim _{\|K\| \rightarrow 0} \frac{\|f(p+h d)-f(p)-\langle\nabla f(p), k\rangle\|}{\|K\|}=0
\end{aligned}$
코멘트 1. gradient vector $\nabla f(p)$는 내적 <$\cdot,\cdot$>의 선택에 의존한다.
만약에 내적에 해당하는 행렬이 $\left(\begin{array}{ll}
1 & 0 \\0 & 1\end{array}\right)$이면 $\nabla f(p)=(\frac{af}{ax}(p),\frac{af}{ay}(p))$임을 알 수있다.
2. 미분가능성의 유도
$\begin{aligned}
& (\nabla f)(p), d\rangle=D_{d} f(p)=\lim _{h \rightarrow 0} \frac{f(p+h d)-f(p)}{h} \\
& \Leftrightarrow \lim _{h \rightarrow 0} \frac{f(p+h d)-f(p)-h\langle\nabla f(p), d\rangle}{h}=0
\end{aligned}$
$\begin{aligned}
& \Leftrightarrow \lim _{h \rightarrow 0} \frac{f(p+h d)-f(p)-h\langle\nabla fcp), d\rangle}{h}=0\end{aligned}$
$\begin{aligned}
& \Leftrightarrow \lim _{h \rightarrow 0} \frac{f(p+h d)-f(p)-h\langle\nabla fp), hd\rangle}{d}=0\end{aligned}$
$\Leftarrow$ 각 $p\in\mathbb{R}^2 $ 마다 $\begin{aligned}\nabla f(p) \\\end{aligned}$가 존재하여
$\begin{aligned}
& \lim_{|K| \rightarrow 0} \frac{\|f(p+h d)-f(p)-\langle\nabla f(p), k\rangle\|}{\|K\|}=0
\end{aligned}$이 된다. 이 형태가 통상적인 다변수 미적분학 책에서 소개하는 미분가능성의 정의이다.
3. 위의 정의를 미분법으로 정의하면 미분가능한 함수는 반드시 연속함수이고 두 미분가능한 함수들의 합성 또한 미분가능한을 보일 수 있다.
4. 미분법이란 주어진 공간이 벡터공간인 여하와 무관하게 공간의 각 점마다 그 점이 원점이 되는 벡터를 만드는 방법들을 지칭한다.
$\langle\nabla f(p), d\rangle=D_{d} f(p)(*)$
의미: $\begin{aligned}\nabla f(p) \\\end{aligned}$는 각 방향 $d$마다 $d$ 방향의 미분계수를 출력해주는 멕터이다.
- 함수 $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}$를 시각화하기 위해서 3차원 공간 $(x, y) \longmapsto f(x, y)=z$ $\mathbb{R}^3=\{(x,y,z)|x,y,z\in\mathbb{R}\}$을 도입하자.

코멘트 일변수 함수 $y=f(x)$의 미분 $f'(x)$을 $x$에서의 기울기로서 직관적으로 해석했었던 것처럼 다변수 함수 $z=f(x,y)$의 미분 역시 직관적으로 살펴볼 수 있다.
대전제 편의를 위한 비약으로서의 가정으로, 이 렉쳐노트에서 사용하는 내적에 대응하는 행렬 $\left(\begin{array}{cc}\langle(1,0),(1,0)\rangle & \langle(1,0),(0,1)\rangle \\\langle(0,1), (1,0)\rangle & \langle(0,1),(0,1)\rangle\end{array}\right)$
은 항상 항등행렬 $\left(\begin{array}{ll}
1 & 0 \\0 & 1\end{array}\right)$을 사용하기로 한다.
이 경우 우리는 내적으로 dot product를 사용한다고 표현하며, 이에 대한 기호로 $<a,b>$대신에 $a\cdot{b}$로 표현하기로 하자.
이 경우에 $a=(a_1,a_2), b=(b_1.b_2)$인 $a,b\in\mathbb{R}^2$에 대해 내적값 $a\cdot{b}$을 구해보면
$a \cdot b=\left(\begin{array}{ll}
a_{1} & a_{2}
\end{array}\right)\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\left(\begin{array}{l}
b_{1} \\
b_{2}
\end{array}\right)=a_{1} b_{1}+a_{2} b_{2}$ 이다.
코멘트 다변수 미분을 직관적으로 이해하는데 가장 요긴한 세 가지 수학적인 대상이 있고 각각 구배 (Gradient), 회전 (Curl), 발산 (Divergence)라 합니다. 이들을 정의하고 직관적으로 살펴보는 것부터 해봅시다.
$f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$ 의 Gradient Vector $\nabla f(P)$
$\nabla f(P)$는 벡터, 즉 $\mathbb{R}^2$의 원소이므로
$\nabla f(P)$=$(a,b)=a(1,0)+b(0,1)$로 표현되는 실수 $a,b\in\mathbb{R}$가 존재한다. (위 페이지의 $(*)$에 의해)
$
\begin{aligned}
& \nabla f(p) \cdot(1,0)=D_{(1,0)} f(p)=\lim _{h \rightarrow 0} \frac{f(p+h(1,0))-f(p)}{h}=\frac{\partial f}{\partial x}(p) \\
& (a, b) \cdot(1,0) \\
& \quad a \cdot 1+b \cdot 0=a, \Rightarrow a=\frac{\partial f}{\partial x}(p),
\end{aligned}$
벡터 (1.0)대신에 (0,1)을 동일한 식 $(*)$에 적용하면
$
\begin{aligned}
& \nabla f(p) \cdot(0,1)=D_{(0,1)} f(p)=\lim _{h \rightarrow 0} \frac{f(p+h(0,1))-f(p)}{h}=\frac{\partial f}{\partial y}(p) \\
& (a, b) \cdot(0,1) \\
& \quad a \cdot 0+b \cdot 1=b, \Rightarrow a=\frac{\partial f}{\partial y}(p)
\end{aligned}$
그러므로 $\nabla f(p)=(a, b)=\left(\frac{\partial f}{\partial x}(p), \frac{\partial f}{\partial y}(p)\right)$ 이다.
Gradient Vector의 직관

f: $\mathbb{R}^{2} \longrightarrow \mathbb{R}^{\prime 2 \prime }$의 회전 (curl)
$f=(f_1(x,y),f_2(x,y)), f_i:\mathbb{R}^2\longrightarrow\mathbb{R},i=1,2$에 대해
$f$ 의 회전은 $\frac{\partial f_{1}}{\partial y}-\frac{\partial f_{2}}{\partial x}: \mathbb{R}^{2} \longrightarrow \mathbb{R}$ 으로 정의한다.

회전 $\frac{\partial f_{1}}{\partial y}-\frac{\partial f_{2}}{\partial x}$의 직관:

$f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2}$ 의 발산 (divergence)
$f=(f_1(x,y),f_2(x,y)), f_i:\mathbb{R}^2\longrightarrow\mathbb{R},i=1,2$
$f$ 의 발산은 $\frac{\partial f_{1}}{\partial y}-\frac{\partial f_{2}}{\partial x}$ 로 정의한다.
발산의 직관: "원전 검줄기 (Source detector)" 함수 $f$가 $x$방향으로 변하는 양 $\frac{af_1}{ax}$와 $y$방향으로 변하는 양 $\frac{af_2}{ay}$더해서 모은 것 입니다.
즉 $f$의 순간적인 '폭발'을 재는 것입니다.

Gradient, Curl, Divergence의 기호화를 위한 ▽
지금까지 Gradient vector에만 사용해온 $\nabla f(p)$의 '역삼각형' ▽ (nobla로 읽는다)를 다음과 같은 벡터 기호로 받아들이자 : $\nabla$=$(\frac{a}{ax},{a}{ay})$.
$f=: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ 의 Gradient Vector : $\nabla{f}=(\frac{\partial f_{1}}{\partial y}-\frac{\partial f_{2}}{\partial x})$
(엄밀하게는 각 벡터 $p∈\mathbb{R}^2$마다 $\nabla f(p)$라고 적어야지만 $(p)$를 생략하고 $\nabla {f}$로 많이 적는다)
$f:(f_1.f_2): \mathbb{R}^{2} \longrightarrow \mathbb{R}^2$ 의 curl $(\frac{\partial f_1}{\partial y}, \frac{\partial f_2}{\partial x})$는
▽×$f$로 표기하자. (사실 엄밀히는 Cross products는 $\mathbb{R}^3$와 $\mathbb{R}^7$에서만 정의되지만 $\mathbb{R}^2$에서 $\mathbb{R}^3$로 일반화하는 것으로서 이 기호를 차용하고자 한다)
$f:(f_1.f_2): \mathbb{R}^{2} \longrightarrow \mathbb{R}^2$ 의 divergence $(\frac{\partial f_{1}}{\partial y}+\frac{\partial f_{2}}{\partial x})$는 dot product $\cdot$을 이용해서 ▽$\cdot(f_1,f_2)로 적자.
정리하면,
$\nabla f=\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)$ - gradient of $f$
$\nabla \times f=\frac{\partial f_{1}}{\partial y}-\frac{\partial f_{2}}{\partial x}$ - curl of $f$
$\nabla \cdot f=\frac{\partial f}{\partial x}+\frac{\partial f_{2}}{\partial y}$ - divergence of $f$
10강 내용은 여기까지 입니다.
이후의 노트는 Gradient ▽, Curl ▽×, Divergence ▽$\cdot$ 에 대한 직관을 잡으신 이후에 재미삼아서 개인적으로 읽으시길 권합니다.
1. 열빙정식 (Heat equation): 현대수학의 출발점
공간 $\mathbb{R}^3$에서 각 $(x,y,z)∈\mathbb{R}^3$마다 그 지점에서 온도를 알려주는 함수 $T:\mathbb{R}^4\longrightarrow\mathbb{R}$가 있다고 하자. (온도 (Temperature)를 따서 T로 적었습니다. t는 시간에 해당하는 변수입니다.)
$(x, y, z, t) \mapsto T(x, y, z, t))$
온도함수 T가 각 $(x,y,z)∈\mathbb{R}^3$에서 만드는 유속은 벡터인 $\nabla T=\left(\frac{\partial T}{\partial x}, \frac{\partial T}{\partial y}, \frac{\partial T}{\partial z}\right)$로 표현하면 될 것이다.
열방정식: $:\frac{aT}{At}=\nabla\cdot\nabla{T}$
즉, 열방정식은 온도의 시간에 대한 변화는 온도가 만드는 벡터가 순간 폭발하는 양과 같아야 함을 미분을 사용해서 표현한 것이다.
열방정식에 대한 이모저모
- 열방정식은 나폴레옹 시대의 프랑스 수학자 푸리에에 의해 제안되었다. 당시에 물리학적으로 열은 유체의 흐름이라는 가설과 입자의 운동이 만든다는 가설이 서로 충돌하고 있었는데, 푸리에의 열방정식은 온도차이 (▽T)가 생기면 열유속이 반드시 생겨야 하는 점에서 열의 물리적 실체가 무엇이든지 사용 가능하다.
- 비록 푸리에는 열방정식의 해를 푸리에 급수 (Fourier Series, 향후에 다룹니다)를 사용해서 해결하였으나 이 접근은 당시의 수학으로는 정당화하는게 불가능했다. 칸토어는 이 푸리에 급수를 고민하면서 현대 수학의 초석인 집합론을 창시한다.
- 한편으로, 열방정식에서 '열'이라는 물리적 실체는 사실 쓰이지 않았고 온도 차이에 따른 열흐름 처럼, 무언가 '유속'만 주어지면 그대로 활용할 수 있다. 전기 이론이서 옴의 법칙(전압=전류X저항)으로 잘 알려진 옴은 열방정식을 참고하여 옴의 법칙을 제안한다.
- 열방정식은 너무나도 방대한 함의를 갖는 방정식이다. 해석학, 확률론, 편미분방정식, 미분기하학, 위상수학, 대수기하학,.... 굉장히 다양한 수학들이 굉장히 비자명한 방식으로 열방정식과 직접적으로 연결된다.
- 수학계에서 열방정식을 사용하여 해결된 밀레니엄 난제 중에 푸앙카레 가설이 있다. 이 가설은 3차원 공간 중에 공간위의 임의의 폐곡선이 한 점으로 수축 가능한 공간은 3차원 구로 변형 가능하냐 는 물음이다. 그레고리 페렐만은 공간 위의 내적들 (리만 메트릭)을 열방정식의 해로서 바라보고 내적들을 바꾸는 과정을 토대로 이 가설이 참임을 증명한다. 이 방법을 리치 흐름 (Ricci flow)라고 부른다.
2. 맥스웰 방정식: 전자기학의 꽃, 현대 물리학의 출발점
총 4개의 방정식으로 구성되어 있다.
- 가우스 법칙: 전하가 있으면 전기장이 존재한다.
$\Leftrightarrow$$\nabla\cdot{E}=\frac{1}{\varepsilon_0}e$, ${\varepsilon_0}$:숫자(=진공중의 유전율=permittivity)
$\begin{aligned}
& E=\left(E_{1}, E_{2}, E_{3}\right): \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \text { (전기장 elictric field) } \\
& \rho: \mathbb{R}^{3} \longrightarrow \mathbb{R}
\end{aligned}$ 전하 (밀도)
2. 가우스 자기 법칙: 자기장의 원천은 존재하지 않는다
$
\begin{aligned}
& \Leftrightarrow \nabla \cdot B=0, \\
& B=\left(B_{1}, B_{2}, B_{3}\right): \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \text { 자장 (magnetic fied) }
\end{aligned}$
3. 패러데이의 법칙: 자기장이 변하면 전기장이 생긴다
$\Leftrightarrow$$\nabla\cdot{E}=\frac{aB}{at}$
4. 앙페어의 법칙: 전기장이 변하면 자기장이 생긴다
$\Leftrightarrow\nabla\times{B}=\frac{\varepsilon_0}{m_0} \frac{aE}{at}+J$, $m_0$:숫자(=진공중의 투전율=permeability) J는 변위 전류라고 한다.
- 맥스웰 방정식은 전기장과 자기장을 통합한 수식이다. 전기장과 자기장의 변화는 동시에 일어나서 힘께 전자기파를 형성하며 공간을 뻗어나간다.
- 특히나, 맥스웰 방정식은 전기장과 자기장의 파동성을 알려주며, 이 방정식에 의해 측정된 전자기파의 속력이 측정된 빛의 속도와 일치하기에 맥스웰은 빛이 전자기파라고 결론내렸다.
- 그런데, 여기서 이상한 문제점이 발생한다. 맥스웰 방정식을 푼 결과로 수학적으로 도출되는 결과로 '빛의 속도는 일정하다'에 이르게 되는 점이다. 왜 이상한가? 이 속도를 관창하는 관측자는 가만히 서 있을 수도, 달리는 차 안에 있어도 된다. 즉 관찰자의 '상대속도'는 자유로이 변할 수 있는데 정작 이와 무관하게 관찰자에게 빛의 속도는 일정해야 한다는 것이다. 왜 이런 모순적인 결론이 가능한가? 시공간에 대한 이해가 잘못되었기 때문이다. (내적을 잘 못 고르고 있었다)
기존의 공간에 대한 이해: $\mathbb{R}^3$가 공간이고 시간은 독립적인 요소이다.
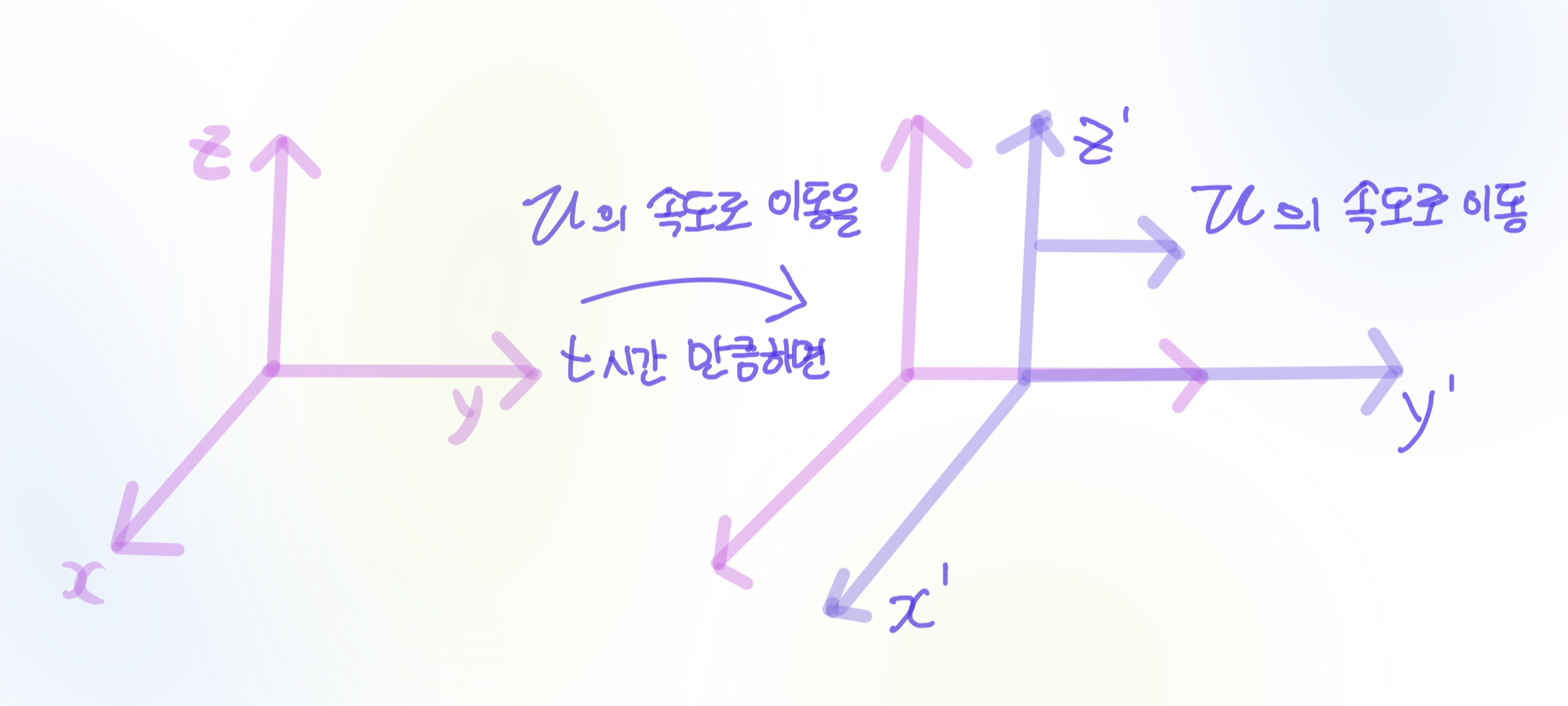
이 빙식으로 $(x, y, z, t)$ 를 다른 좌표계인 $\left(x^{\prime}, y^{\prime}, z^{\prime}, t^{\prime}\right)$로 옮겨주는 것. 이 방정식은 행렬로 표현 가능하며, 이 행렬들의 모임은 군 구조를 가지며 이를 갈릴레이 군 (Galilean group) 이라고 부른다. 맥스웰 방정식은 갈릴레이 군을 사용하면 안 되는걸 알려준다.
그래서 빛의 속도가 상수로 유지가 되게끔 위의 군구조를 수정한 것을 로렌츠 군 (Lorentz group)이라 부르며,
로렌츠 군과 호환되는 시공간을 민코프스키 시공간 $\mathbb{R}^{3,1}$(Minkowski Space)라고 부른다. 민코프스키 시공간의 내적 (리만메트릭)은 쌍곡기하학 (Hyperbolic Geometry)구조를 갖는다. 지금까지 말한 내용이 아인슈타인의 특수 상대성 이론 (Special Relativity Theory)이다.
- 그런데, 지금까지 한 이야기는 빛이 맥스웰 방정식에서 나오는 전자기파, 즉 '파동'이라는 해석 하에서 타당한 것이다. 그러나 알고보니 사실 빛은 '입자'로도 볼 수 있음이 알려지기 시작한다 (양자역학, Quantum Mechanics). 수학적으로는 $n$이 무한대인 경우의 $n×n$ 행렬의 고유치 이야기 이다.
다음 이야기 : 적분의 정의
'직장인과 문과생을 위한 수학교실 (직문수)' 카테고리의 다른 글
| 12,13,14강. 다변수 미분법의 직관에 대한 설명 (0) | 2023.08.05 |
|---|---|
| 11. 미적분학의 기본정리와 적분의 아름다움 (0) | 2023.08.05 |
| 9강. 현대수학에서 미분법의 직관과 의미 (0) | 2023.08.04 |
| 8강. 선형대수학의 꽃, 무지개 정리 (0) | 2023.08.04 |
| 7강. 선형대수학과 기하학 (0) | 2023.08.03 |



