다음 포스팅은 https://youtu.be/srJ0U6bHrCI 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
강의 12,13 미적분학의 기본정리로 직관적으로 이해하는 다변수 미적분학
복습 (11강)
미적분학의 기본정리 (Fundamental Theorem of Calculus)
미분가능한 함수 $f: \mathbb{R} \longrightarrow \mathbb{R}$ 가 주어졌다고 가정하자.
그러면 $a<b$인 두 실수에 대하여 다음이 성립한다:
$\int_{a}^{b} f^{\prime}(x) d x {=} f(b)-f(a)$
$\int_{a}^{b} f^{\prime}(x) d$ 열린 구간 $(a,b)$ 위에서 주어진 함수 $y=f'(x)$의 그래프의 면적의 크기
$f(b)-f(a)$ 미분해서 $f'(x)$가 되는 함수 $y=f(x)$에 대해 열린 구간 $(a,b)$의 양 끝점 $a,b$의 두 함수값 $f(a)$, $f(b)$의 차이

그래프 안쪽을 $(a,b)$를 $n$등분해서

각 직사각형의 밑변을 구성하고,
각 직사각형의 높이를 $y=f'(x)$의 함수값으로 지정해서 $n$개의 직사각형의 넓이를 더하고,
$n$값을 무한대 ∞로 바꾸는게 $\int_{a}^{b} f^{\prime}(x) d x$의 의미이다.
관찰 윗장에서 한 이야기는 함수 $y=f'(x)$의 그래프의 면적을 채우기 위해서 그래프의 내부를 무한개의 직사각형들의 넓이의 합으로 구해나가면, 그 결과가 놀랍게도 미분해서 $f'(x)$가 되는 함수 $y=f(x)$의 $(a,b)$의 양 끝점 $a,b$의 함수값의 차이이다.
상상을 위한 복습 (10강)
Gradient Vector의 직관

$f: \mathbb{R}^{2} \longrightarrow \mathbb{R}$ 의 회전 (curl)
$f=(f_1(x,y),f_2(x,y))$, $f_i: \mathbb R_{2} \longrightarrow \mathbb R,i=1,2$에 대해
$f$의 회전은 $(\frac{\partial f_1}{\partial y}- \frac{\partial f_2}{\partial x})$:$\mathbb{R}^{2}\longrightarrow \mathbb{R}$으로 정의한다.
$\frac{\partial f_1}{\partial y}$ $f$의 $x$성분 함수 $f_1$의 $y$ 방향으로의 변화
$\frac{\partial f_2}{\partial x}$ $f$의 $y$성분 함수 $f_2$의 $x$ 방향으로의 변화

회전 $(\frac{\partial f_1}{\partial y}- \frac{\partial f_2}{\partial x})$의 직관:

결과적으로 반시계 방향으로의 순간 회전의 의미임을 유추/상상할 수 있다
$f: \mathbb{R}^{2} \longrightarrow \mathbb{R}$의 발산 (divergence)
$f=\left(f_{1}(x, y), f_{2}(x, y)\right), f_{i}: \mathbb{R}^{2} \rightarrow \mathbb{R}_{i=1,2}$에 대해
$f$의 발산은 $(\frac{\partial f_1}{\partial x}+ \frac{\partial f_2}{\partial y})$로 정의한다.
발산의 직관: "원천 검출기"(Source Detector)"
함수 $f$가 $x$방향으로 변하는 양 $(\frac{\partial f_1}{\partial x}$와 $y$방향으로 변하는 양 $\frac{\partial f_2}{\partial y})$을 더해서 모은 것 입니다.

즉$f$의 순간적인 '폭발'을 재는 것입니다.
$\mathbb{R}^2$에서 $\mathbb{R}^3$로 확장
- 대전제: 내적에 대응하는 행렬로 항등행렬을 사용. 즉 $a=(a_1,a_2,a_3), b=(b_1,b_2,b_3), a,b∈\mathbb{R}^3$에 대해 $a\cdot{b}:=a_1,b_1+a_2b_2+a_3b_3$로 정의하자. (여전히 $||a||:=\sqrt{a\cdot{a}},a\cdot{b}=||a||\cdot{||b||\cdot{cos\theta}}$를 사용한다)
1) Gradient ▽$f$
$f: \mathbb{R}^{3} \longrightarrow \mathbb{R}$ , $f=f(x,y,z)$에서
$\nabla f_{0}=\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right): \mathbb{R}^{3} \longrightarrow \mathbb{R}^{3}$
의미
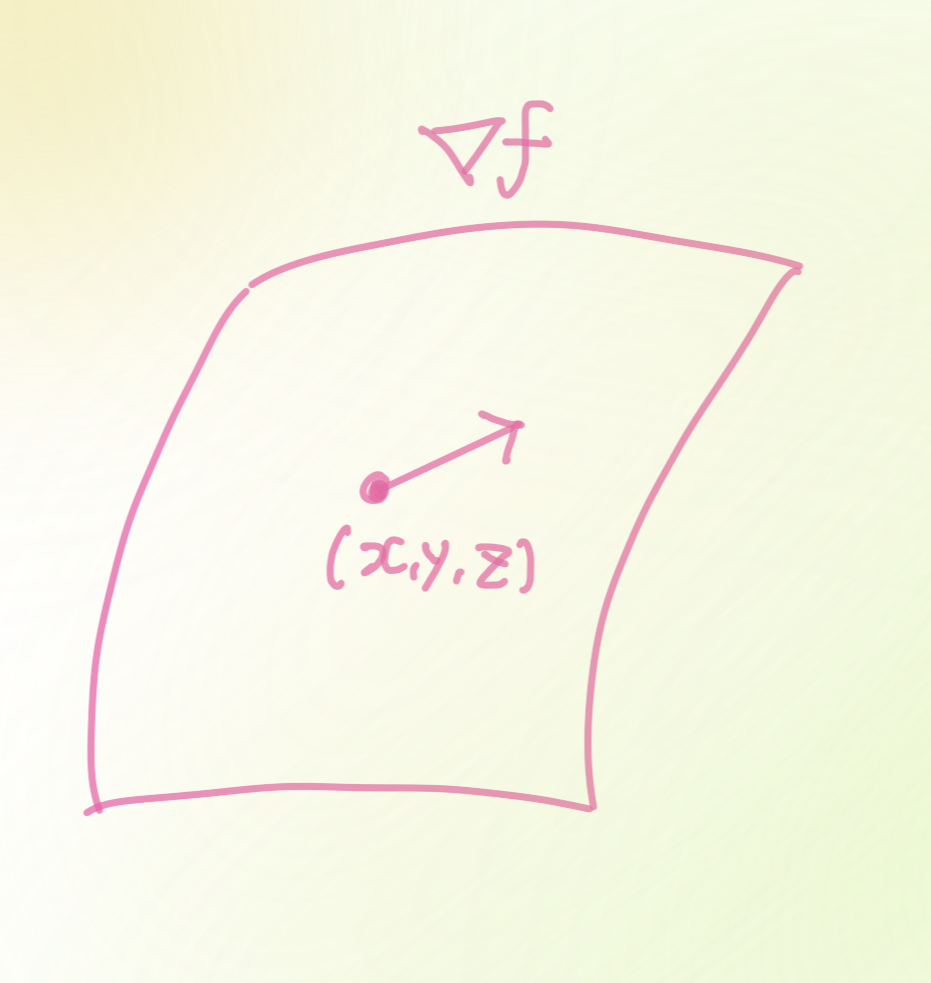
각 점 (벡터) $(x,y,z)$위에서 $f$로 만든 곡면 위에서의 접벡터를 의미
2) Curl off ▽×$f$
$f=\left(f_{1}, f_{2}, f_{3}\right): \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}, f_{i}=f_{i}(x, y, z), i=1,2,3$에서
$\nabla \times f:=\left(\frac{\partial f_{3}}{\partial y}-\frac{\partial f_{2}}{\partial z}, \frac{\partial f_{1}}{\partial z}-\frac{\partial f_{3}}{\partial x}, \frac{\partial f_{2}}{\partial x}-\frac{\partial f_{1}}{\partial y}\right)$
$: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$
의미

각 축을 따라서 회전하는 양을 각 성분으로 하는 벡터 (즉 함수값은$\mathbb{R}^{3}$원소)
3) Divergence ▽×$f$
$f=\left(f_{1}, f_{2}, f_{1}\right): \mathbb{R}^{3} \rightarrow \mathbb{R}$에서
$\nabla \cdot f:=\frac{\partial f_{1}}{\partial x}+\frac{\partial f_{2}}{\partial y}+\frac{\partial f_{3}}{\partial z}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{1}$
의미
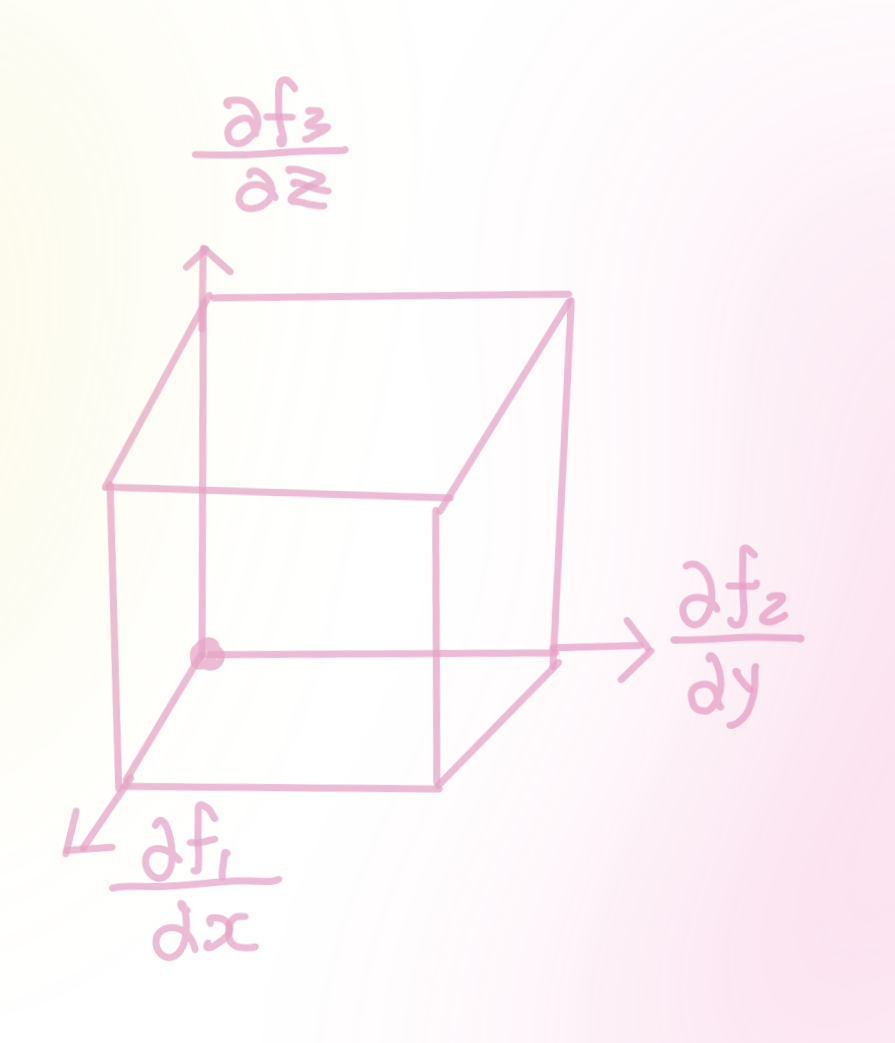
순간적으로 $(x,y,z)$축으로 폭발하는 총량의 재는 함수
$\nabla{f}$, $\nabla×f$, $\nabla\cdot{f}$의 정의가 직관적으로 와닿으신 후에 다음에 대해서 상상해보셨으면 합니다.
가령 아래의 상황에서도 미적분학의 기본정리는 적합한 형태로 성립해야 하지 않을까요?
1) "선적분 (Line Integral)에 대한 미적분학의 기본정리"
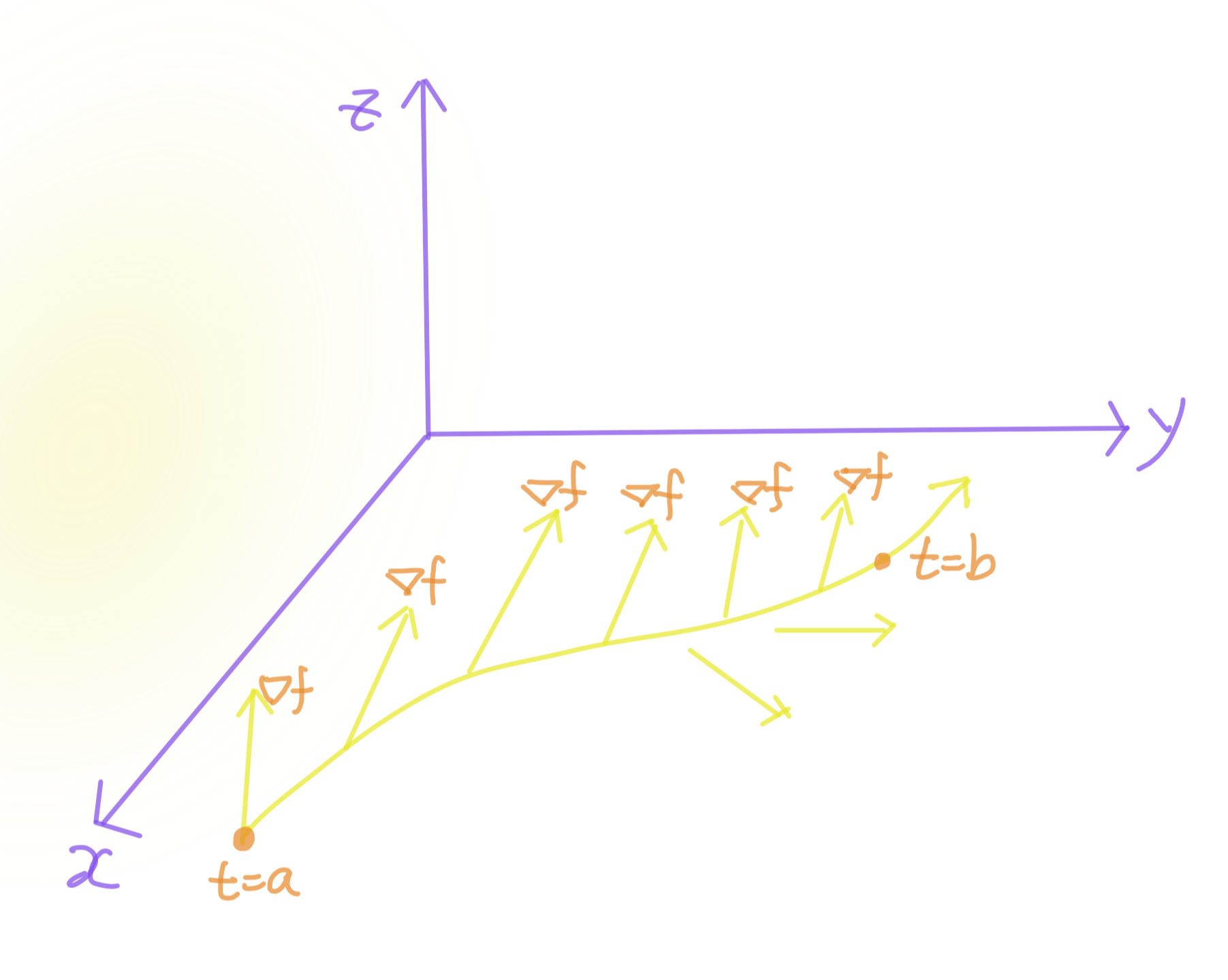
$x$축 위의 $(a,b)$대신에 $x-y$평면 위에 곡선이 놓여 있고, $(a,b)$위에서 함수값 f'(x)가 있었던 것 대신에 $x-y$ 평면위의 곡선의 각 점마다 Gradient Vector ▽×$f$가 놓여있는 것.
2) "그린 정리"

1. 에서 임의의 곡선을 생각했던 것과 달리 폐곡선 (곡선의 시점과 종점이 일치)을 고려하고 폐곡선의 내부 영역을 포함하여 각 점마다 화살표 (벡터장이라 부른다)가 주어진 것.
3) "스토크스 정리"
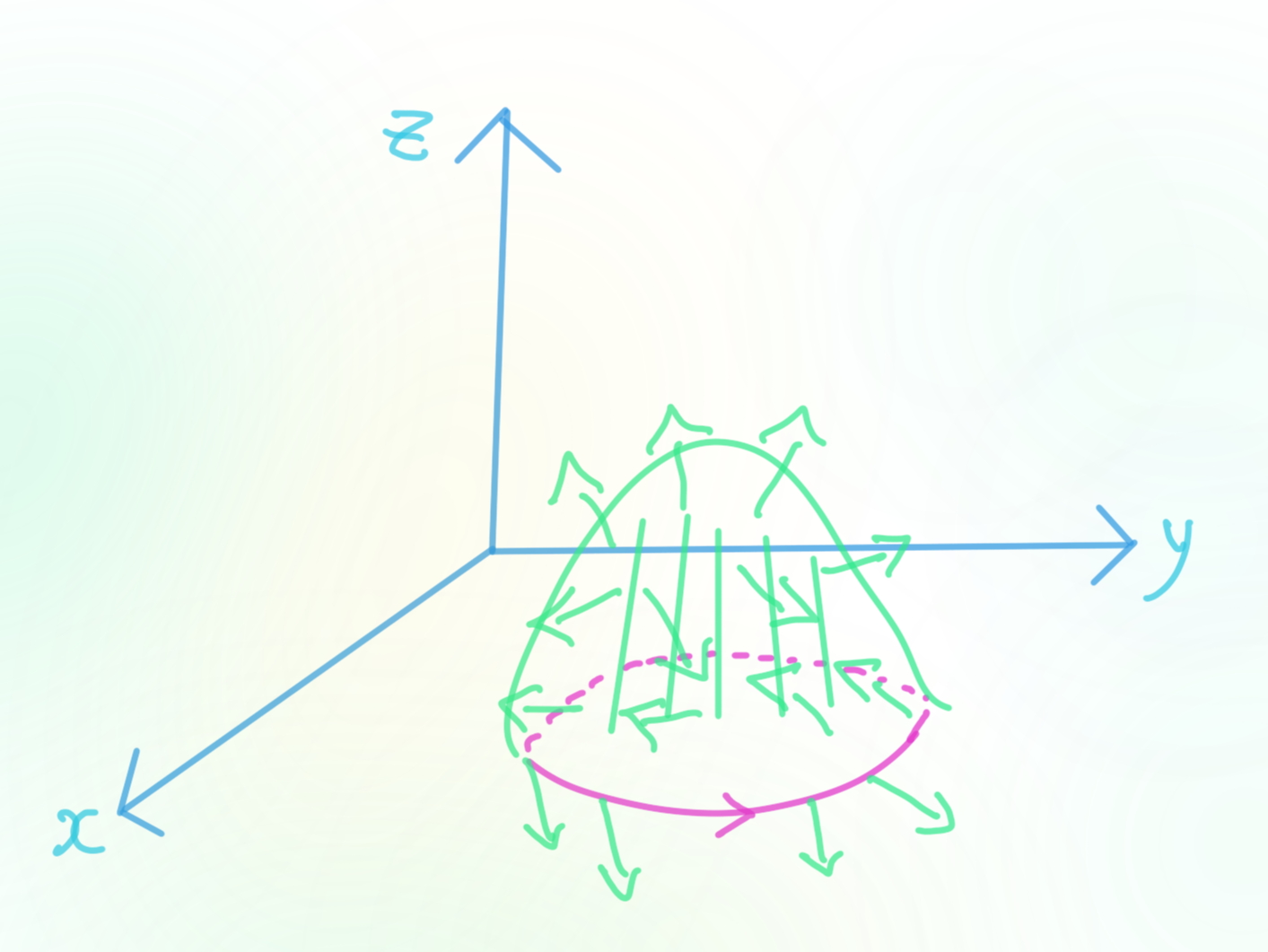
곡면 (껍데기)가 주어져 있고 곡면의 경계 (분홍색 곡선) 을 포함해서 곡면 위의 각 점마다 화살표 (벡터장)가 주어진 것.
4) "발산 정리"

이번에는 3.의 곡면의 내부가 채워져 있다고 가정하고 이 3차원 곡면의 각 점마다 화살표 (벡터장)가 주어진 것.
이 렉쳐의 목적 위의 그림들이 결국 미적분학의 기본정리와 완전히 동일한 관점으로 이해할 수 있음을 직관적으로 살펴보는 것.
미적분학의 기본 정리의 세 가지 구성요소

A. '적분의 정의' $\int_a^{b}f'(x)dx:$
'직사각형 $n$개의 넓이를' 구한 후에 $n$을 무한대 ∞로 확장하는 것.
B. '미분'해서 함수 $y=f'(x)$가 되는 또 다른 함수 $y=f(x)$가 있어야 한다.
C. $f'(x)$를 적분 할 때에는 열린구간 $(a,b)$ 전체가 필요하나 $f(x)$의 함수값을 구할 때에는 $a,b$의 '경계면'에 해당하는 두 점 $a,b$만 필요함

A,B,C가 충족되면 $\int_a^{b}f'(x)dx=f(b)-f(a)$가 성립.
미적분학의 기본정리가 성립하려면 적어도 A-C가 필요하니 이를 기준으로 위에서 살펴본 그림 1-4를 다시 살펴봅시다.
그림 1 선적분에 대한 미적분학의 기본정리
원하는 면적을 구하기 위해서 내부를 직사각형들로 분할해서 이들의 넓이로 근사해나가는 것이 적분이다. 이 개념을 곡선 $r=r(f)$위에서 만든 것을 선적분 (line integral)이라고 부른다.

열린 구간 $(a,b)$가 위 그림에선 분홍색 곡선으로 바뀌었지만 여전히 이 곡선을 $n$등분하여 분할해서 '넓이'를 구한 후에 $n$을 무한대 ∞로 보내면 될 것이다.
여기서 한 가지 고민해야 하는 문제가 있다. $\int_a^{b}f'(x)dx$의 경우에는 $(a,b)$를 $n$등분한 후에 직사각형들의 넓이를 구하기 위해 직사각형의 높이로 함수값 $f'(x)$를 사용할 수 있었는데, 그림 1에서 곡선 위의 각 점에서 주어진 것은 화살표(벡터)이고 이들은 숫자가 아니다.
그러면 직사각형 '높이' 및 '면적'을 어떻게 정의해야 타당한지에 대한 물음이 생긴다.
$x-y$ 평면에서 곡선 $r=r(t)$의 $n$ 등분:

그런데 우리는 두 벡터 $(r_{k+1}-r_k)$, ▽$f(r_k)$가 주어지면 '내적'을 사용해서 두 벡터로부터 특정 값을 만들어 낼 수 있음을 알고 있다.
'내적'을 사용해서 두 벡터로부터 특정값을 만들어낼 수 있음을 알고있다.
그러므로 각 직사각형의 면적의 대체제로서 ▽$f(r_k)\cdot(r_{k+1}-r_{k}) (유클리드 내적) 을 사용하자.
이 후에는 동일하게 $n$을 무한대 ∞로 보낼때 특정값이 된다면, 우리는 이를 곡선 $r=r(t)$, $a≤t≤b$의 벡터장 ▽$f(r(t))$위에서 선적분이라 말하고 $\int_a^{b}\nabla{f}\cdot{dr}$로 표기한다.
이제 적분은 정의가 되었으니 필요조건 B를 생각해보자.
미분해서 '$\nabla{f}$'가 되는 함수를 찾을 수 있는가?
그 함수는 당연히 (미분의 정의에 의해) 주어진 함수 '$f$'일 수 밖에 없다.
마지막 필요 조건 C에 대해 생각해보자. 곡선 $r=r(t)$의 경계면은 곡선의 시점과 종점인 $r(a)$와 $r(b)$이다.
미적분학의 기본정리를 유도한 것과 비슷한 과정을 거치면 다음을 얻는다:
선적분에 대한 미적분학의 기본정리
$\int_{a}^{b} \nabla f \cdot d r=f(r(b))-f(r(a))$
그림 2 그린정리 (Green's Throrem)
그림 1,2는 모두 $x-y$평면 위에서만 (즉 $z$축과 무관한) 곡선들을 살펴보고 있는 것이되, 그림 2의 곡선은 그림 1과 달리 반드시 폐곡선(시점과 종점이 일치)이어야 한다.
폐곡선 조건을 요구하는 이유는 필요조건 C를 다음과 같이 변경하기 위해서이다:

적분하는 영역: 곡선 $r=r(t)$ $a≤t≤b$
적분하는 영역의 경계면:$r(a),r(b)$

적분하는 영역:폐곡선의 내부 영역
적분하는 영역의 경계면: 폐곡선 $r=r(t)$
그림 2의 상황에서 새로운 미적분학의 기본정리를 만들어내기 위해서 폐곡선 및 폐곡선의 내부 영역의 각 점마다 벡터를 출력하는 함수 $F=F(x,y)=(M(x,y),N(x,y))$로 적자.
(보통 벡터장 Vector field로 불리운다)
그림 1의 선적분의 정의를 따라서 $\int_{r(a)}^{r(b)} F \cdot d r$ $F\cdot{dr}$는 잘 주어져 있다고 가정하자. 우리가 알고자 하는 관계는 다음과 같다:
$F$와 관련있는 함수를 폐곡선의 내부 영역에서 적분 = $\int_{r(a)}^{r(b)} F \cdot d r$ .
(우리가 정의해야 하는 것: 필요조건 A,B)

$\int_{r(a)}^{r(b)} F \cdot d r$ 이 지칭하는 것은 벡터장 $F$가 폐곡선을 따라 선적분한 양 ($F$라는 함수가 폐곡선을 따라서 만드는 그래프의 면적처럼 생각)이다.
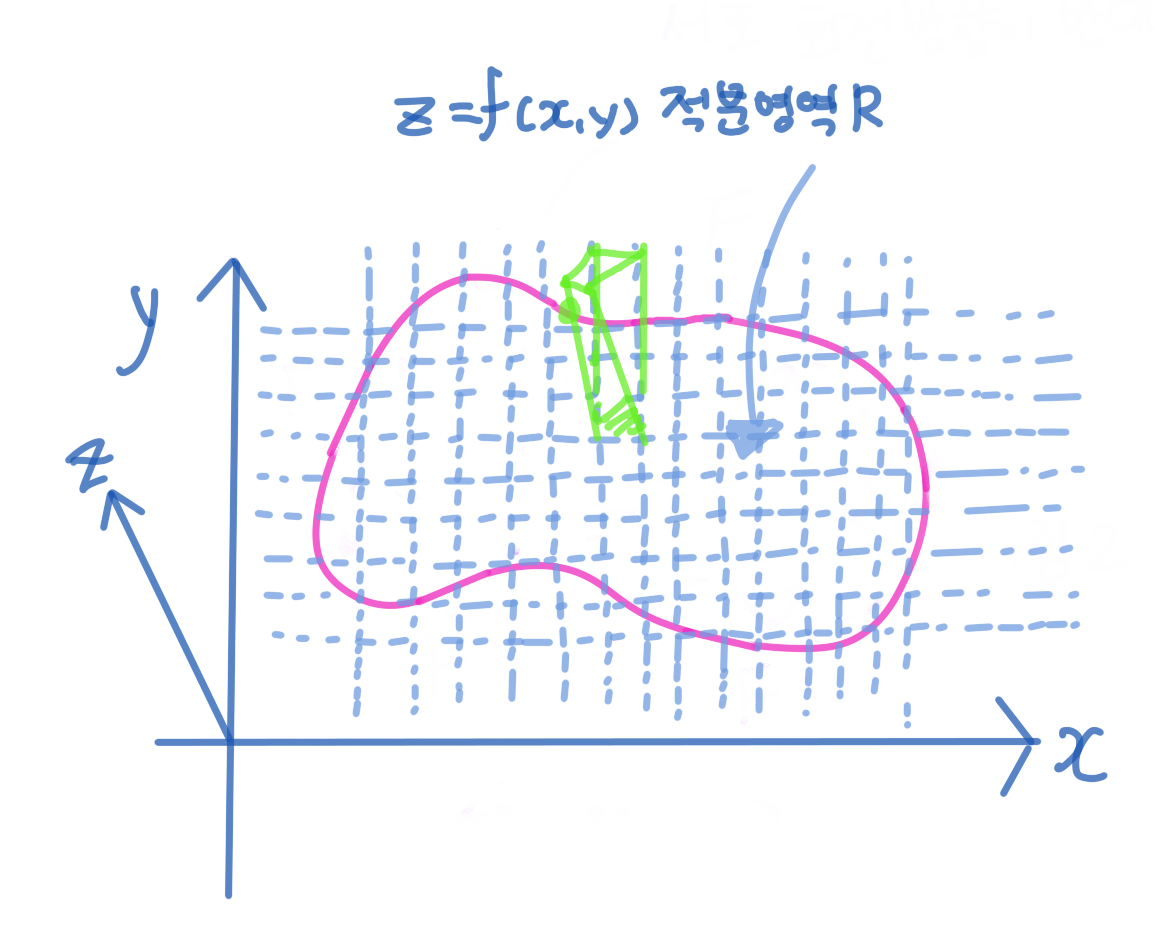
함수 $z=f(x,y)$가 폐곡선의 내부 영역에 주어질 때의 적분의 정의는 $(a,b)$를 $n$개의 '구간'으로 분할했던 것처럼 폐곡면을 $n$개의 '구간'으로 분할했던 것처럼 폐곡면을 $n$개의 '직사각형'으로 분할하고, 각 직사각형 위에서 함수 $f$의 함수값을 높이로 갖는 직육면체를 만들어서 이 부피들을 다 더하고 $n$을 무한대로 늘리는 것을 의미한다.
이를 $\iint_{R} f(x, y) d x d y$로 적고 '이중적분'(double intergal)이라고 부른다.
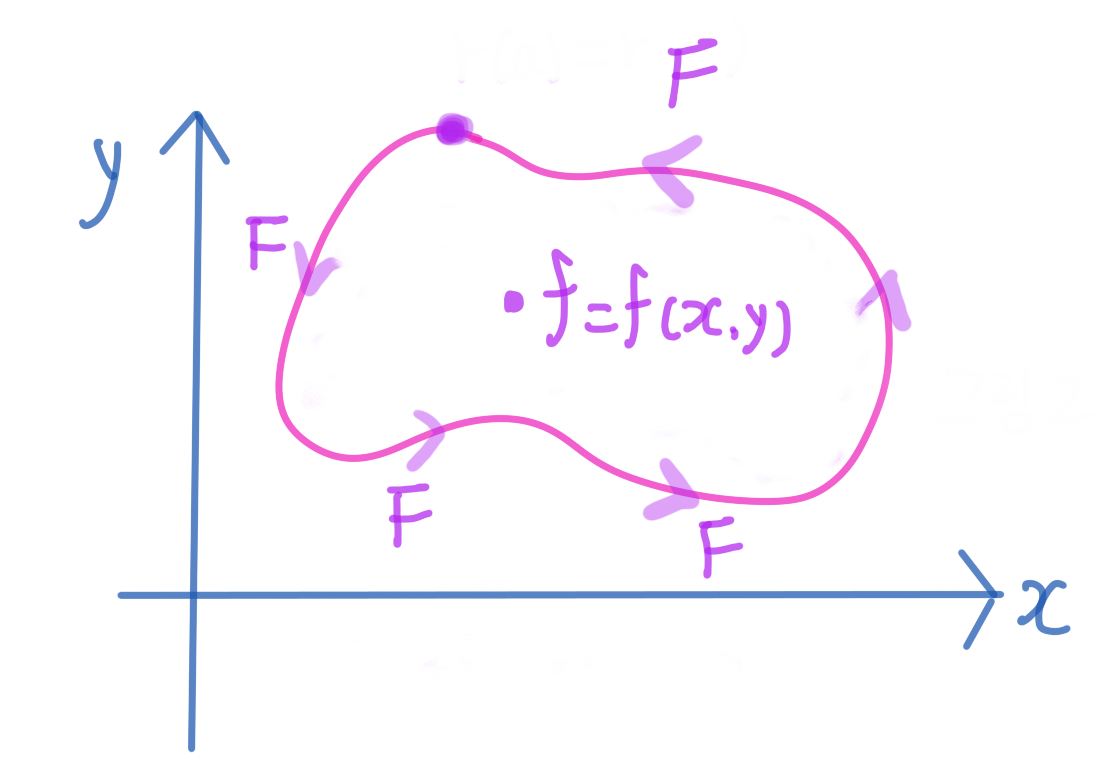
그러면 폐곡선의 내부 영역에서 어떤 함수 $z=f(x,y)$의 이중적분 $\iint_{R} f(x, y) d x d y$와 폐곡선을 따라 벡터장 $F=(M,N)$의 적분인 $\int_{r(a)}^{r(b)} F \cdot d r$이 관계를 맺겠는가?
즉, $\iint_{R} f(x, y) d x d y$=$\int_{r(a)}^{r(b)} F \cdot d r$인 $f=f(x,y)$는 무엇인가?
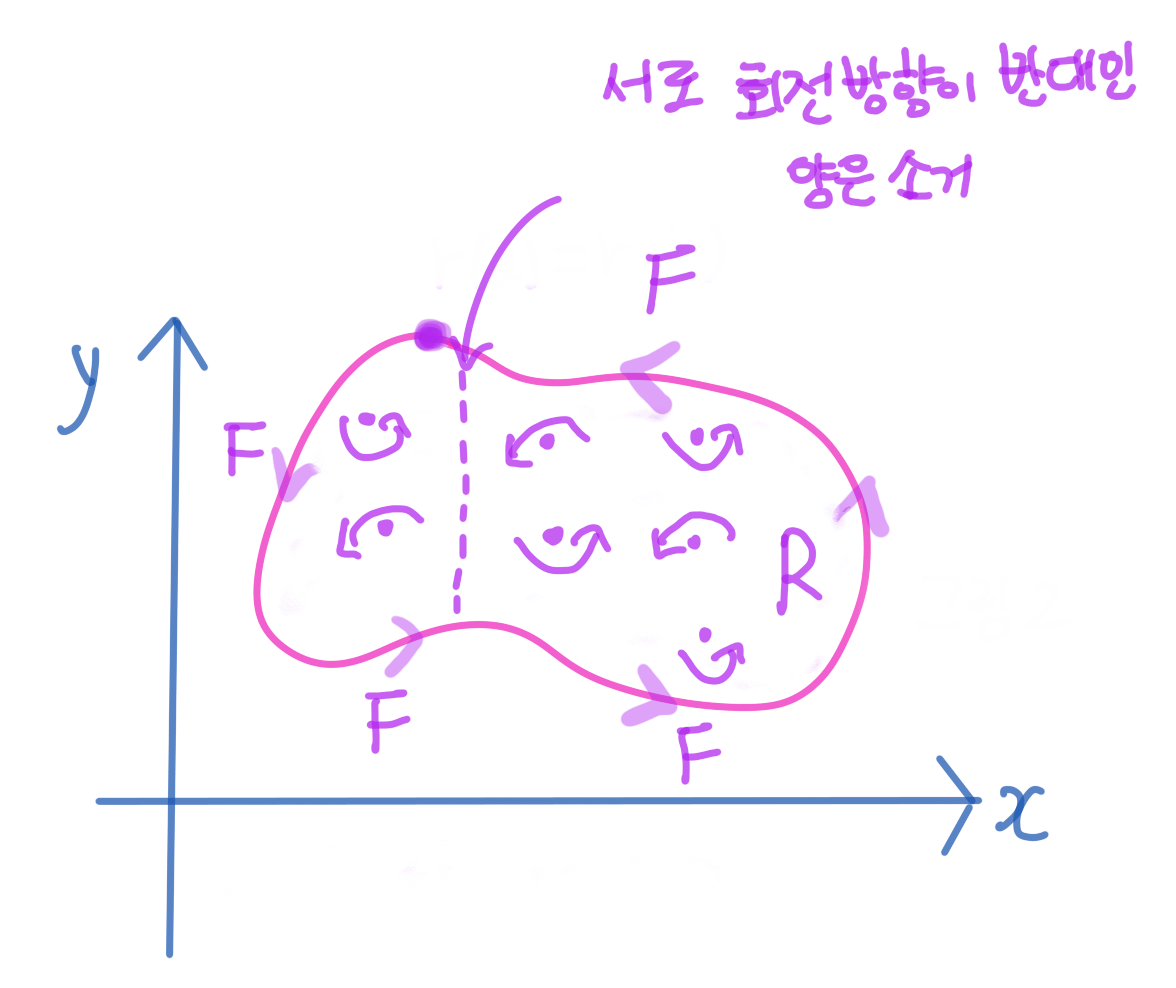
이 답에 대한 직관은 다음과 같다. 폐곡선 내부에서 $F$가 '회전'하는 양들을 재자. 참고로 우리는 벡터장 $F=F(x, y)$ $=(M(x, y), N(x, y))$ 의 회전이 $\frac{\partial M}{\partial y}-\frac{\partial N}{\partial x}$임을 알고 있다(10강).
폐곡선 내부에서 $F$의 회전하는 양을 전부 모으면 (즉 $F$의 회전을 영역 $R$에서 이중적분하면) 서로 회전하는 방향이 반대인 양들은 전부 소면되고 결국에는 영역 $R$의 경계면에 해당하는 폐곡선 위에서 $F$의 선적분만 남게 될 것이다.
우리는 지금까지 다음의 정리를 직관적으로 살펴본 것이다:
그린의 정리 (Green's Theorem)
폐곡선 $r=r(t),a≤t≤b$, $r(a)=r(b)$ 내부의 영역을 $R$이라 하자. 폐곡선 및 $R$위에서 임의의 벡터장 $F=F(x,y)=(M(x,y),N(x,y))$이 주어지면 다음이 성립한다: $\iint_{R}$$\frac{\partial M}{\partial y}-\frac{\partial N}{\partial x}dxdy=\int_{r(a)}^{r(b)} F \cdot d r$
그림 3. 스토크스의 정리 (Stoke's Theorem)
Stoke's theorem은 Green의 정리를 아주 조금 변형하는 것에 지나지 않다. 폐곡선의 내부가 $x-y$평면에 속해야 했던 가정만 배제하기로 하자.

이 경우에는 그림 2에서 이중적분을 정의할 때 폐곡면을 $n$등분한 직사각형들이 옆의 그림처럼 위치하게 된다. 각 직사각형들이 같은 평면위에 주어지지 않으므로 이 직사각형들을 직육면체의 밑으로 사용하기 위해서는 각 직육면체의 높이를 새롭게 지정해줘야 할 것이다.
이를 위해서 곡면 (껍데기) $S$의 각 점 마다 접평면을 세우고, 그 접평면에 수직이고 크기가 1인 벡터 $N$을 고려하자:

우리는 3차원 공간 위에서 벡터장
$F=\left(F_{1}(x, y, z), F_{2}(x, y, z), F_{3}(x, y, z)\right)$의 회전이 $\nabla \times F$로 주어지는 것을 알고 있다.
그러므로 벡터 $N$ 및 내적을 사용하여 "$\nabla \times F\cdot{N}$"을 ($F$의 회전 curl이 접평면에 수직인 방향의 크기)
직육면체의 높이로 사용하게 되면 나머지는 이중적분에서 한 방식과 동일하게 이렇게 구성한 이중적분에서 한 방식과 동일하게 이렇게 구성한 직육면체들의 부피를 더 더하고 $n$을 무한대로 바꾸면 껍데기 $S$위에서 $F$$(\nabla×F)$양을 다 더한 의미가 될 것이다.
이를 $\iint_{s} \nabla \times F \cdot N d s$로 적고 $(\nabla×F)$의 면적분(surface intergal)이라 부른다.
코멘트 임의의 벡터장 $F=(F_{1}, F_{2}, F_{3})$에 대해 곡면 $S$위에서의 면적분 $\iint_{s} F \cdot N d s$도 위와 동일한 방식으로 정의하면 된다.
- 그린의 정리와 동일한 직관에 의해 다음이 성립함을 유추할 수 있다:
스토크스의 정리 (Stoke's Theorem)
폐곡선 $r=r(t), a≤t≤b, r(a)=r(b)$가 주어지고 이 폐곡선이 경계면이 되는 곡면 (껍데기) $S$가 $\mathbb{R}^3$에 주어져 있다고 가정하자. 그러면 $S$에서 정의된 임의의 벡터장 $F=(F_{1}(x, y, z), F_{2}(x, y, z), F_{3}$에 대하여 다음이 성립한다:
$\iint_{s} F \cdot N d s$=$\int_{r(a)}^{r(b)} F \cdot d r$
그림 4. 발산 정리 (Divergence Theorem)
스토크스의 정리에서 사용한 곡면 $S$를 3차원 내부의 경계면으로 바라볼 때의 미적분학의 기본정리를 '발산 정리'라고 한다.
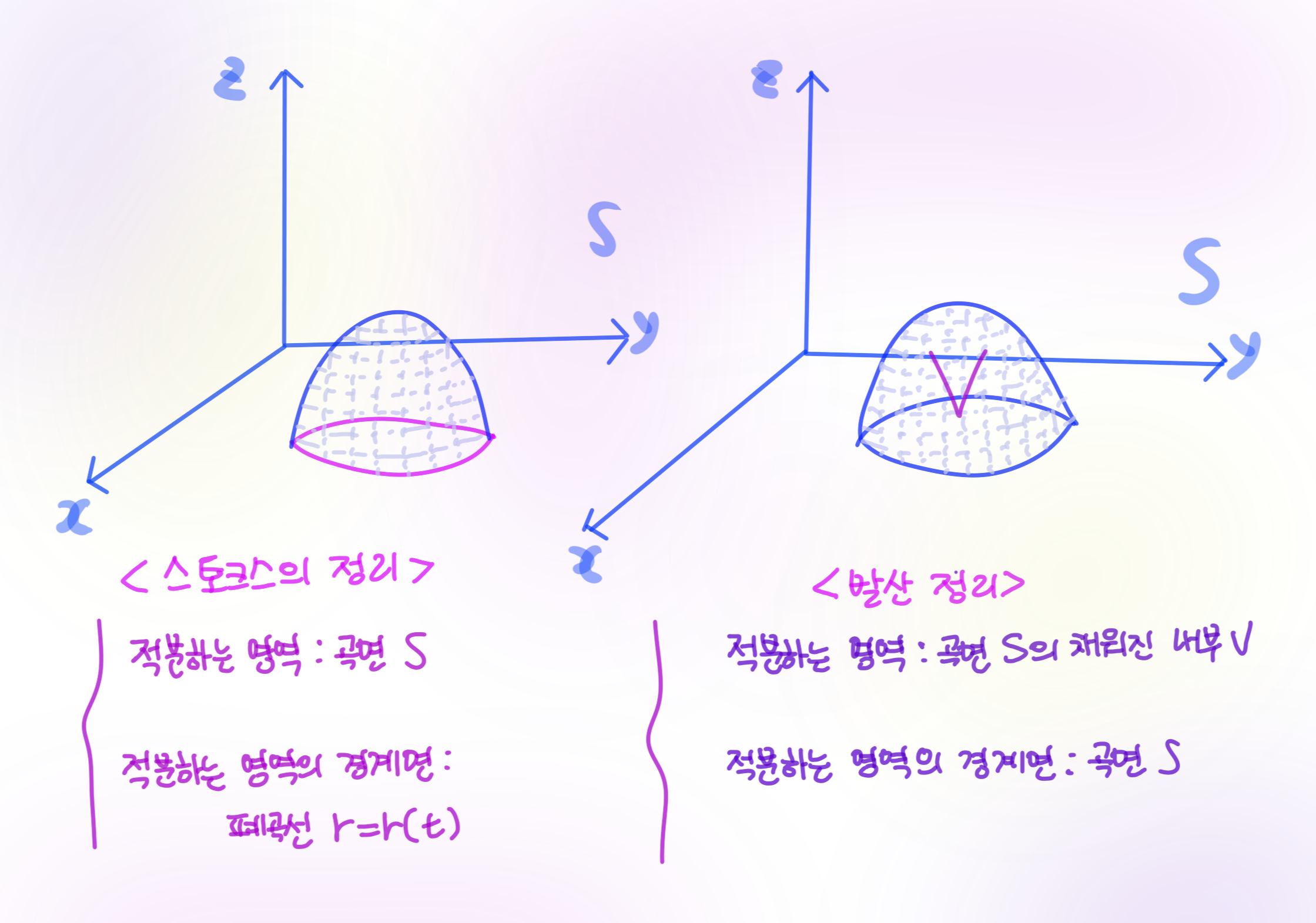
이번에는 곡면 $S$의 3차원 내부를 적분해야 한다. 지금까지 해온 방식과 완전히 동일한 방식으로 3차원 내부를 $n$개의 '직육면체'로 분할하고 각 직육면체 '위에' 함수값을 높이로서 곱한 '4차원' 부피를 구한 뒤에 이들을 더해나가서 정의하는 적분을
삼중적분 (Triple Integral)이라고 부르며,
함수 $f=f(x,y,z)$의 3차원 영역 $V$에서의 삼중적분을 $\iiint_{V}\cdot f(x, y, z) d x d y d z$로 표기한다.
우리가 찾고자 하는 함수 $f=f(x,y,z)$는 다음을 만족하는 함수이다:
$\iiint_{V}\cdot f(x, y, z) d x d y d z$=$\iint_{S} F \cdot N d S$
$\iiint_{V}\cdot f(x, y, z) d x d y d z$= 함수 $f=f(x,y,z)의 3차원 공간 $V$위에서 '그래프'의 총 '부피'
$\iint_{S} F \cdot N d S$= 벡터장 $F=(F_{1}, F_{2}, F_{3})$이 3차원 공간 $V$의 경계면인 $S$를 따라서 빠져나가는 양
직관은 $F$가 경계면으로 빠져나가는 양은 $F$가 내부에서 '폭발' 하는 총량과 같아야 할 거라는데 있다. 그런데 $F$의 폭발은 바로 $\nabla\cdot F$이므로 우리는 다음의 정리를 얻는다:
발산정리 (Divergence Theorem)
폐곡면 $S$의 내부 영역을 $V$라 하자. 그러면 $V$및 $S$에서 정의되는 임의의 벡터장에 대해서 다음이 성립한다:
$\iiint_{V} \nabla \cdot F(x, y, z) d x d y d z=\iint_{S} F \cdot N d S$
14강 미분기하학의 아름다움
'직장인과 문과생을 위한 수학교실 (직문수)' 카테고리의 다른 글
| 16. 리만의 복소함수론과 대수기하의 아름다움 (0) | 2023.08.07 |
|---|---|
| 15강. 미분기하의 아름다움 (0) | 2023.08.06 |
| 11. 미적분학의 기본정리와 적분의 아름다움 (0) | 2023.08.05 |
| 10. 다변수 미분법의 직관적 이해와 수학, 물리학의 현대적 태동 (0) | 2023.08.05 |
| 9강. 현대수학에서 미분법의 직관과 의미 (0) | 2023.08.04 |



