다음 포스팅은 https://youtu.be/YdnBQaY5eDk 의 영상에서 작성한 노트의 핵심을 정리한 것입니다. 여러 오탈자 및 수정 사항들이 있을 수 있습니다. 노트 내용에 대한 디테일한 설명들은 영상을 참고하시길 바랍니다.
Monotone Convergence Theorem (MCT). Let $(a_{n})_{n=1}^{\infty}$ be a monotone increasing sequence (i.e., $\forall n \in \mathbb{N}, a_{n} \leq a_{n+1}$ ).
$$
\begin{gathered}
\text { Then } \exists \lim _{n \rightarrow \infty} a_{n}=\sup \left\{a_{n} \mid n \in(N\}\right. \\
\operatorname({inf})
\end{gathered}
$$
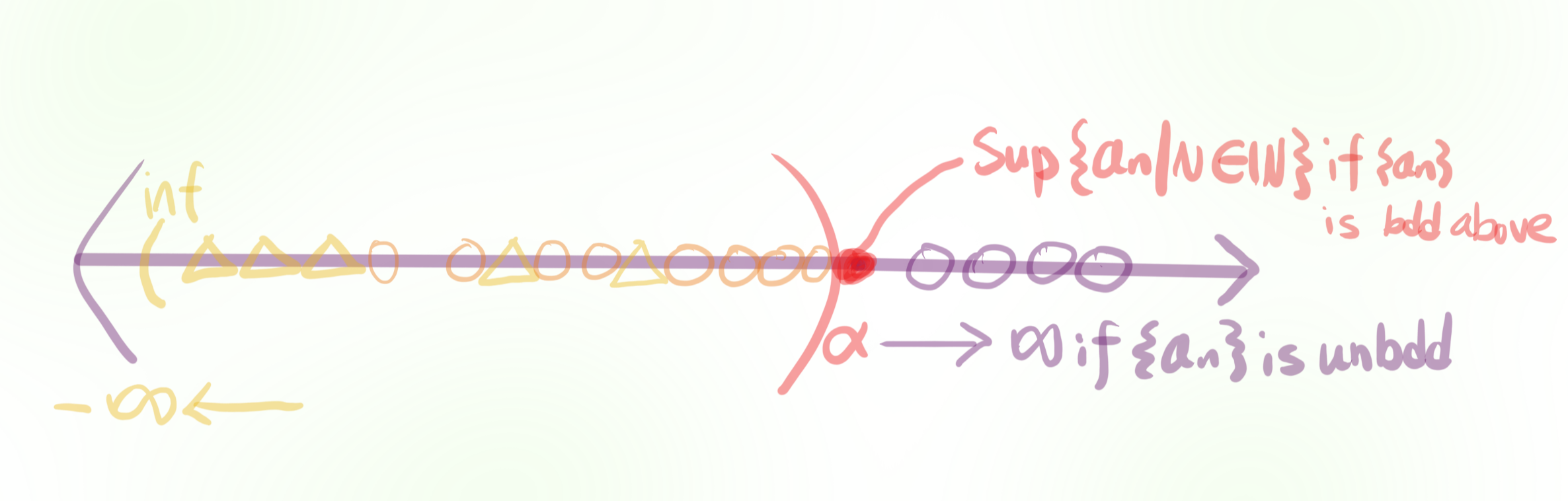
Proof. Suppose $\{a_n\}$ is monotone increasing and bounded above
Consider $\phi \neq\left\{a_{n} \mid n \in \mathbb{N}\right\} \subseteq \mathbb{R}$ : bounded above
By LUP, $\left.\exists \sup \leqslant a_{n} \ln \in \mathbb{N}\right\}=: \alpha \in \mathbb{R}$
Claim: $\lim _{n \rightarrow \infty} a_{n}=\alpha$
Fix any $\varepsilon>0$
Then $x-\varepsilon$ is not an upper band of $\{a_n | \in \mathbb{N}\}$
Thus $\exists N \in \mathbb{N}$ set $x-\varepsilon<a_{N}$
since $\left\{a_{n}\right\}$ is monotone increasing, $\forall n \geq N$,
$$
\alpha-\varepsilon<a_{N} \leq a_{n} \leq \alpha<\alpha+\varepsilon
$$
$$
\Rightarrow \forall n \geq N, \quad\left|a_{n}-x\right|<\varepsilon
$$
We have shown that $\lim _{n \rightarrow \infty} {a_n}=\sup \operatorname{a}_{n}[n \in \mathbb{N}\}$ provided is bounded above.
If $\left\{a_{n} \mid n \in \mathbb{N}\right\}$ is not bounded above, (*)
$$
\text { Claim: } \lim _{n \rightarrow \infty} a_{n}=\infty
$$
Fix any $M \in \mathbb{R}$
From the assumption (*), there exists $N\in \mathbb{N}$ such that $a_N\geq M$.
Since $(a_n)$ is monotone increasing,
$$
\forall n \geq N, \quad a_{n} \geq a_{N} \geq M.
$$
Thus $\forall M \in \mathbb{R}, \exists N \in \mathbb{N}$ set $\forall_{n \geq N}, a_{n} \geq M$.
$\Leftrightarrow \lim _{n \rightarrow \infty} a_{n}=\infty$.
Exercise. Prove Monotone Convergene Theorem if a sequence is monotone decreasing
Remark. Least Upper Bound Property $\Rightarrow$ Monotone Convergence Theorem $\Leftrightarrow$ Nested Interval Property. In fact, all of them are equivalent.
{Nested. Interval Property}. If $(I_{n})_{n=1}^{\infty}$ is a sequence of bounded closed intervals such that $I_{n+1} \subset I_{n}$ for all $n \in \mathbb{N}$. Then $\bigcap_{n=1}^{\infty} I_{n} \neq \varnothing$.

Proof. Denote $I_{n}=\left[a_{n}, b_{n}\right], \forall_{n} \in \mathbb{N}$
Since $I_{n} \geq I_{n+1}, a_{n} \leq a_{n+1} \leq b_{n+1} \leq t_{n}, \forall_{n} \in \mathbb{N}$.
$$
\begin{aligned}
& \stackrel{\forall n, m \in \mathbb{N}}{\Rightarrow} a_{n} \leq a_{n+1} \leq \cdots \leq a_{n+m} \leq b_{n+m} \leq \ldots \leq b_{m} \\
& \Rightarrow \forall n_{m} m \in \mathbb{N}, \quad a_{n} \leq b_{m}: \text { eliminate the } \\
& \text { dependency of indices. }
\end{aligned}
$$
Since $\{a_n | \in \mathbb{N}\}$ is monotone increasing, and bdd above by MCT,
$$
\exists \lim _{n \rightarrow \infty} a_{n}={\sup _{n \in \mathbb{N}} a_{n} \leq b_{m}} \quad \forall m
$$
In particular, $\{b_n | \in \mathbb{N}\}$is bdd below, monotone - decreasing
$$
\begin{gathered}
\stackrel{M C T}{\Rightarrow} \lim _{m \rightarrow \infty} b_{m}=\inf _{\frac{M \in \mathbb{N}}{g \cdot l \cdot b}} f_{m} \\
\Rightarrow \sup _{n \in \mathbb{N}} \leq \inf _{m \in \mathbb{N}}
\end{gathered}
$$
Note that $\forall n \in \mathbb{N}$,
$$
\begin{aligned}
& a_{n} \leq \sup _{n \in \mathbb{N}} a_{n} \leq \inf _{m \in \mathbb{N}} b_{m} \leq b_{n} \\
\Rightarrow & \phi \neq \bigcap_{n=1}^{\infty} I_n,
\end{aligned}
$$
and $\left[\sup _{n \in N} a_{n}, \inf _{m \in N} b_{m}\right] \subset \bigcap_{n=1}^{\infty} I_n$.
'기초부터 대학원 수학까지, 해석학개론' 카테고리의 다른 글
| 12. 해석학개론 (g) Limsup, Liminf (0) | 2023.07.31 |
|---|---|
| 7. 해석학개론 (d) 극한정리 (0) | 2023.07.25 |
| 6. 해석학개론 (c) 수열의 수렴성 (0) | 2023.07.25 |
| 5. 해석학개론 (b) 유리수의 조밀성과 실수, 자연수 공리 (0) | 2023.07.25 |
| 4. 해석학개론 (a) 완비성 공리 (the least upper bound property) (0) | 2023.07.24 |

